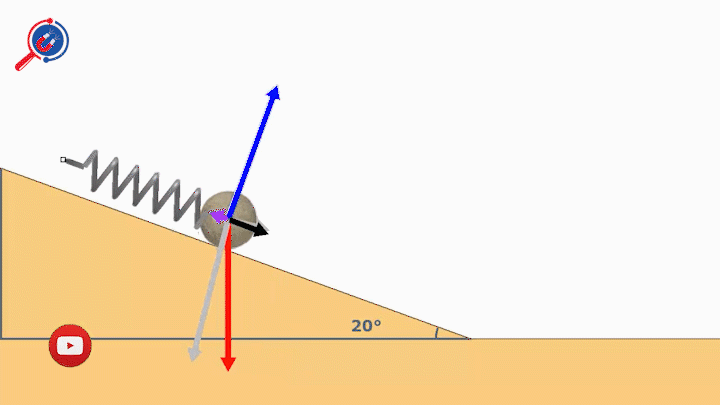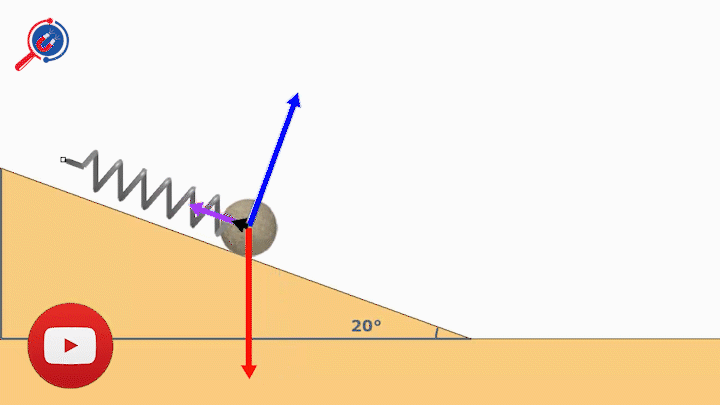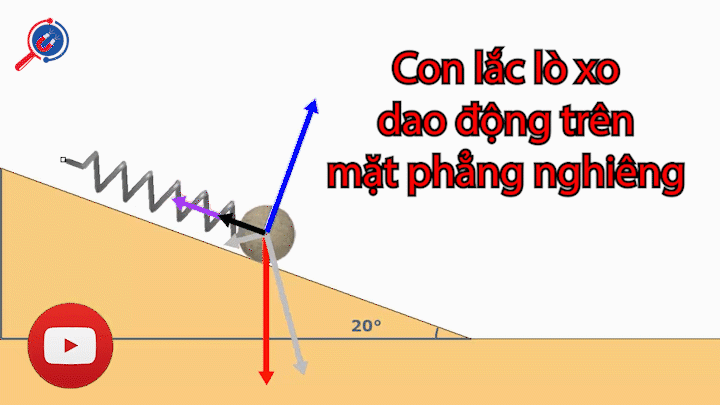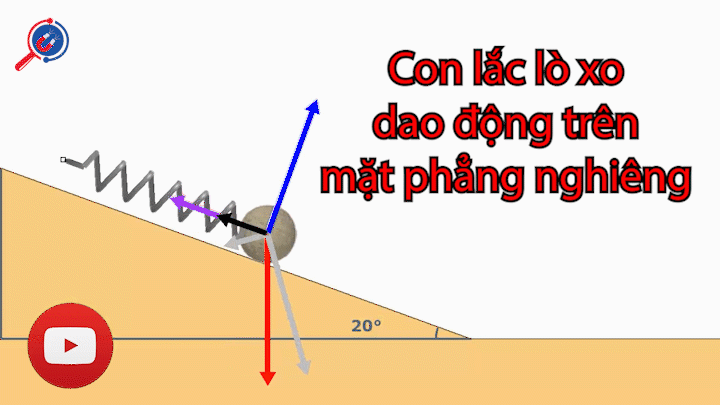
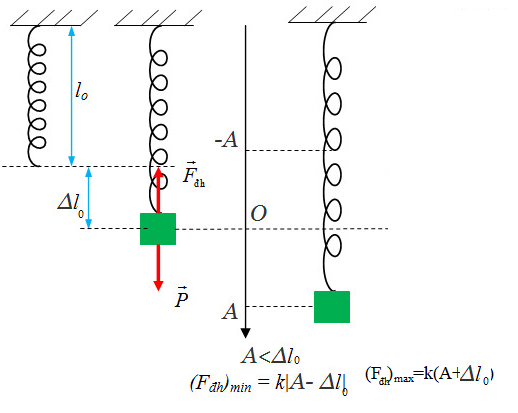
Chú thích:
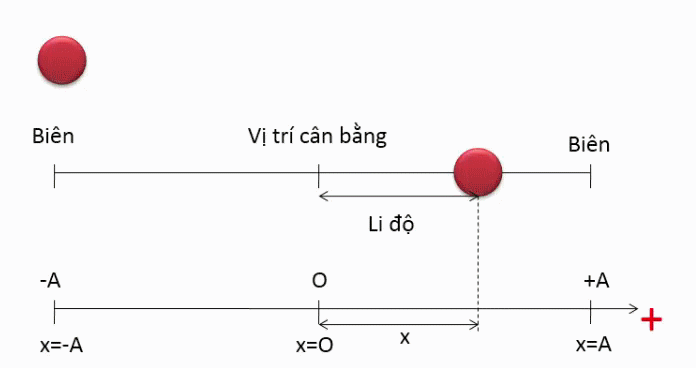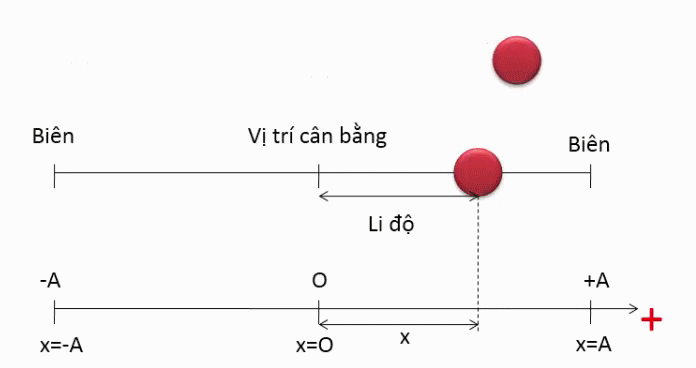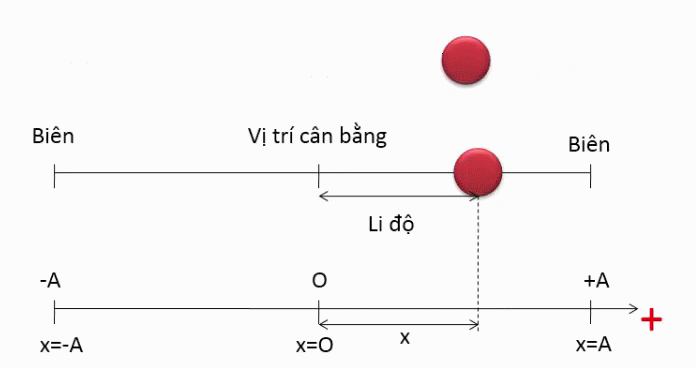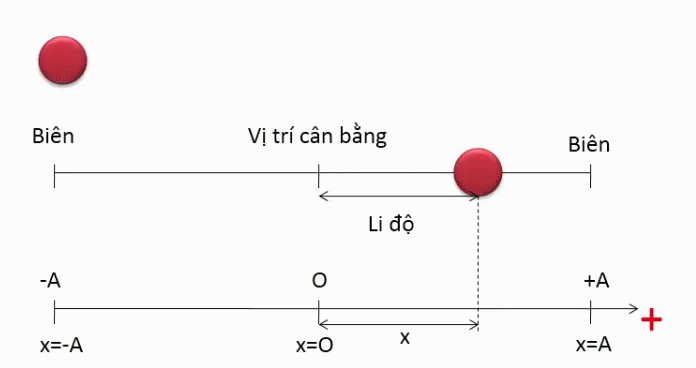
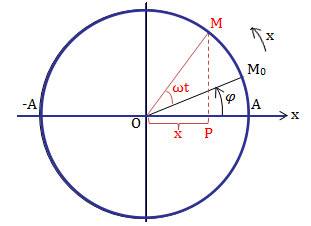
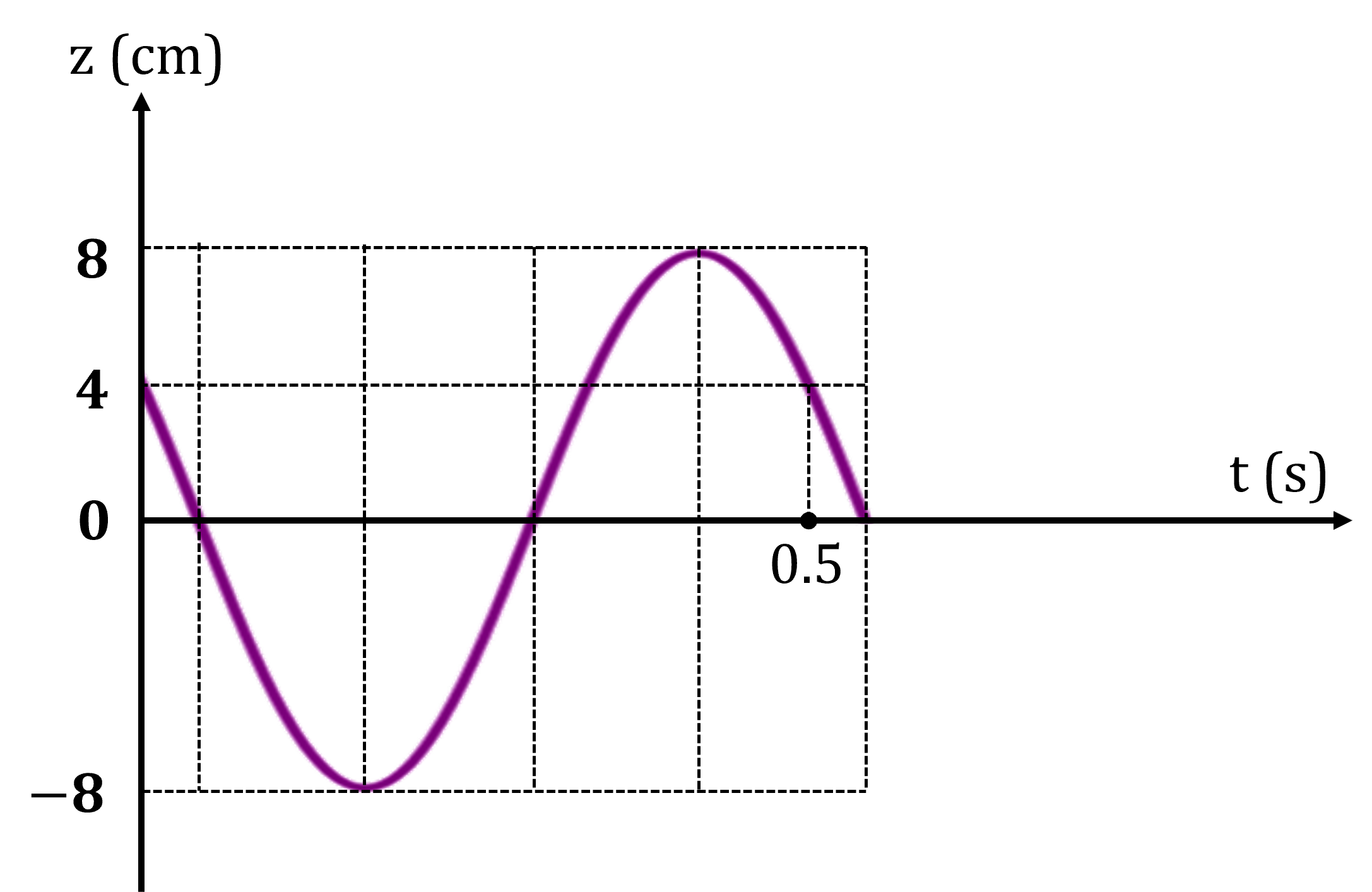
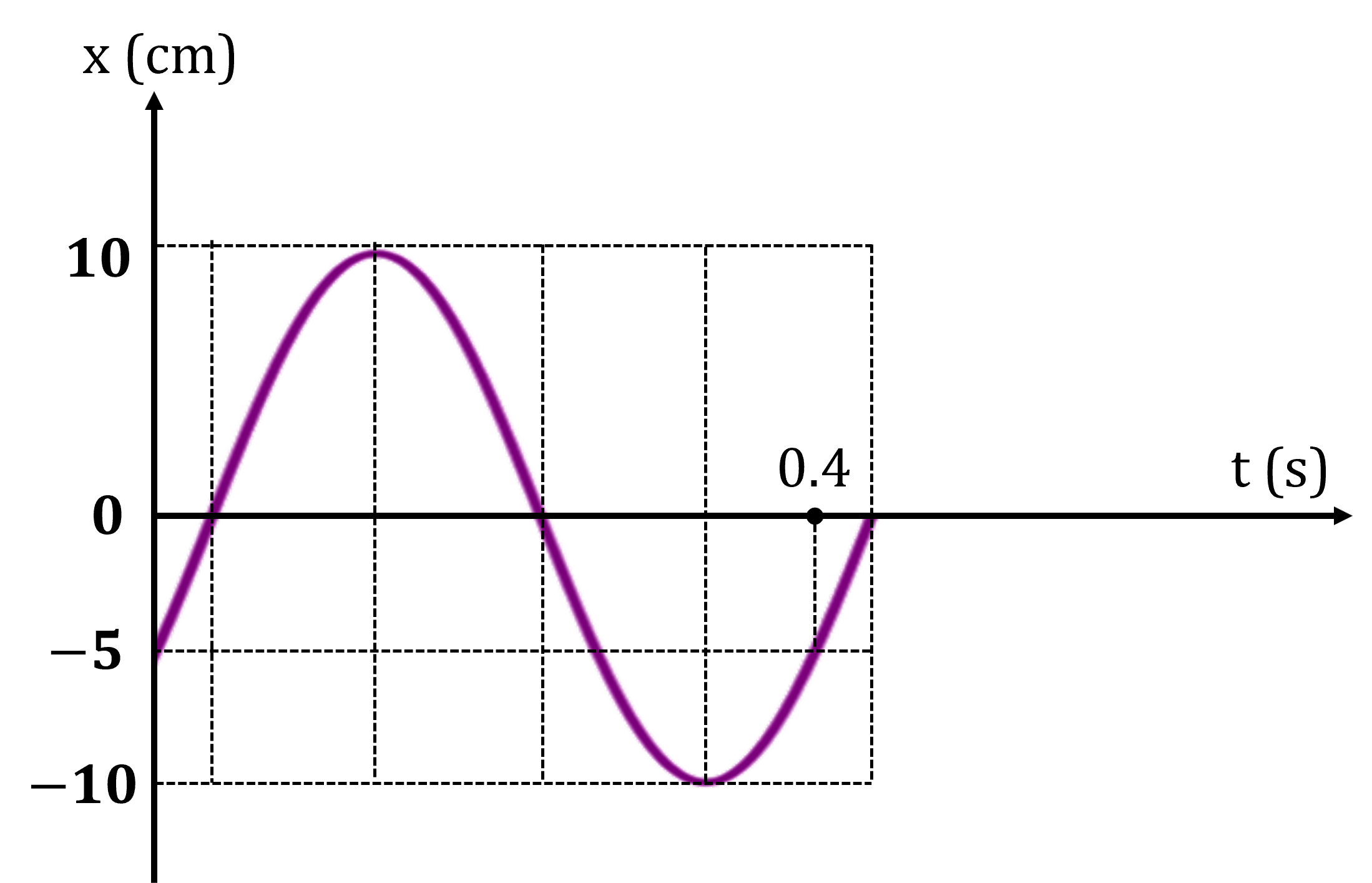
: Li độ của chất điểm
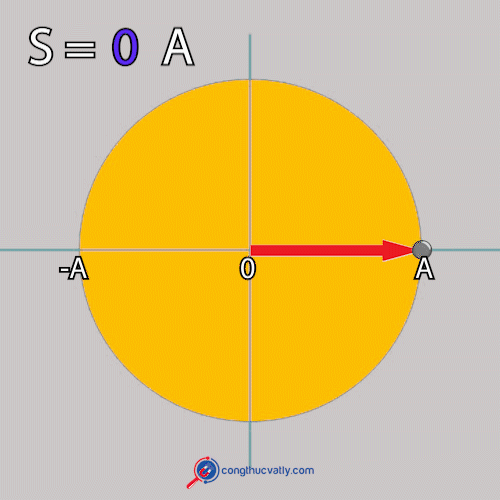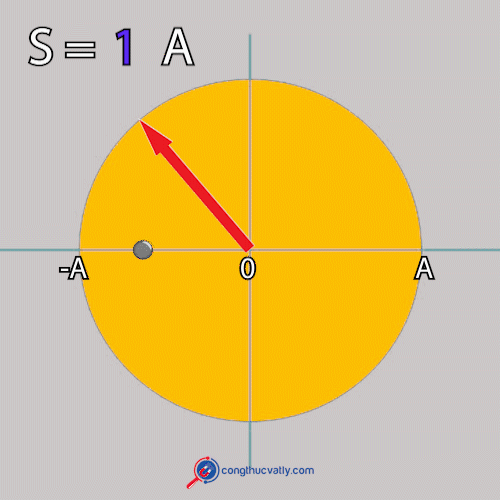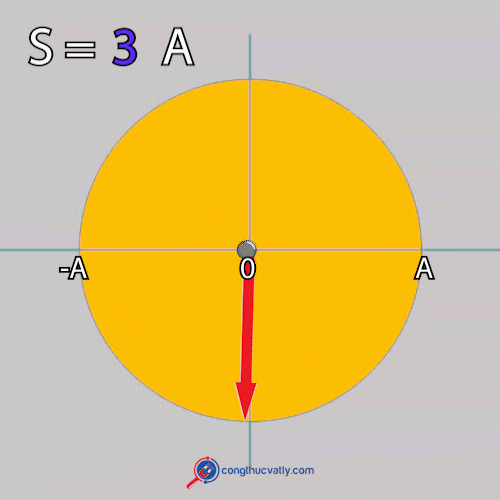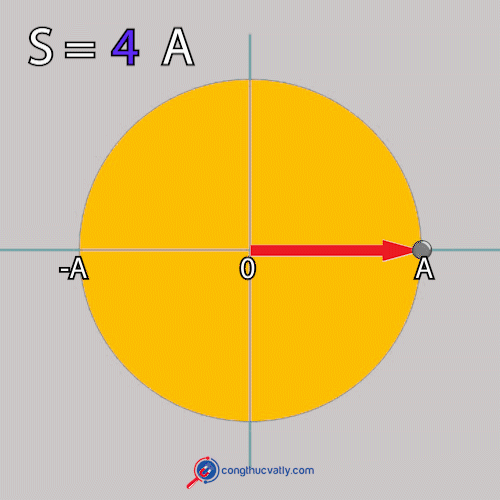
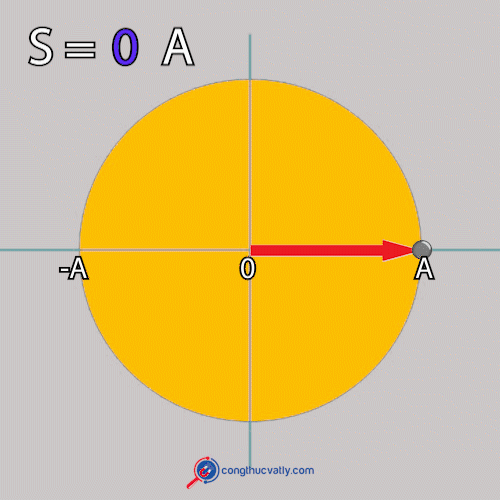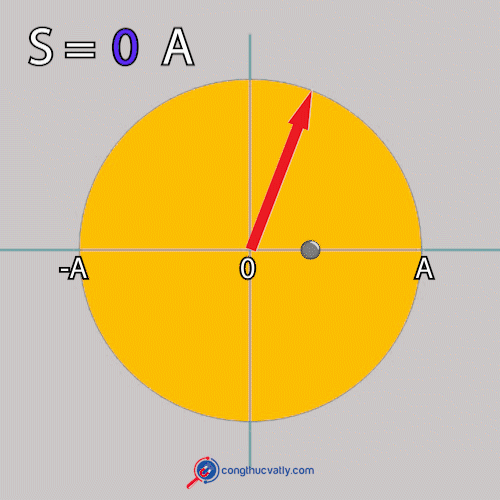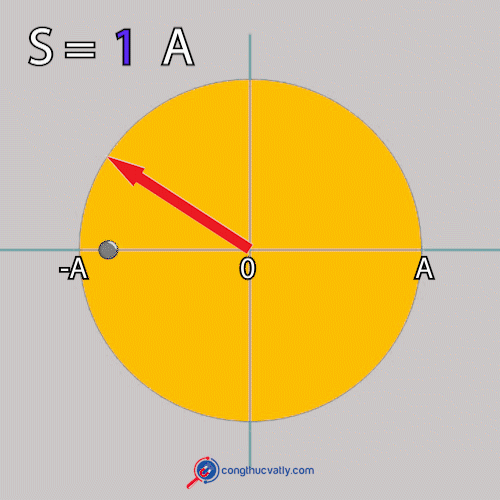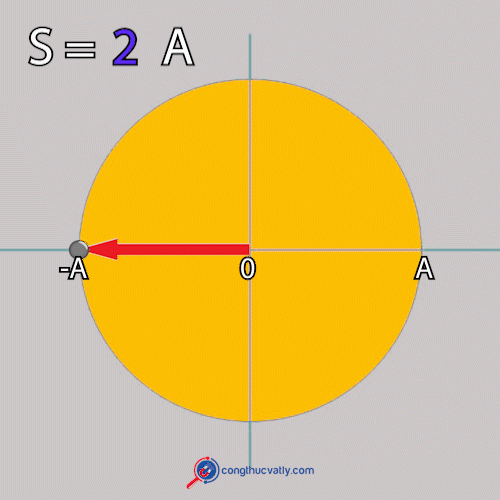
: Độ dài quỹ đạo
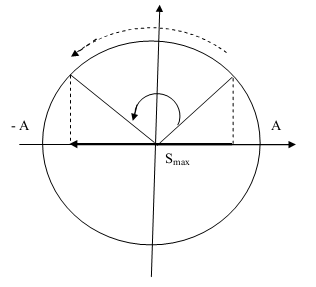
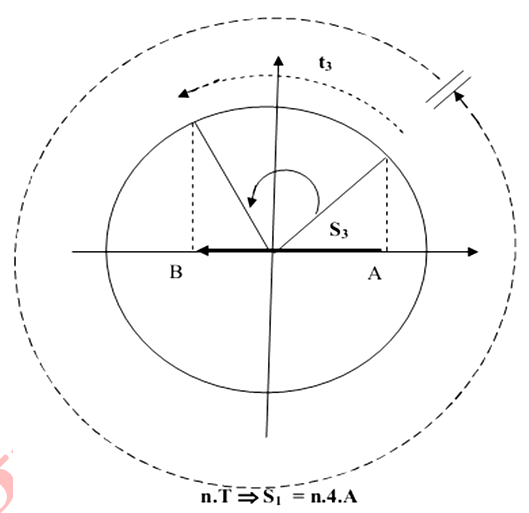
: Quãng đường vật đi được trong vòng
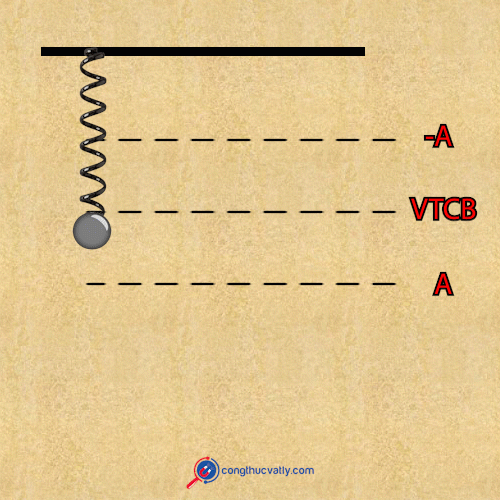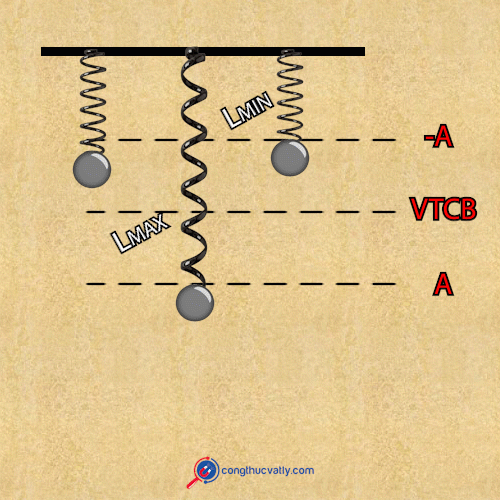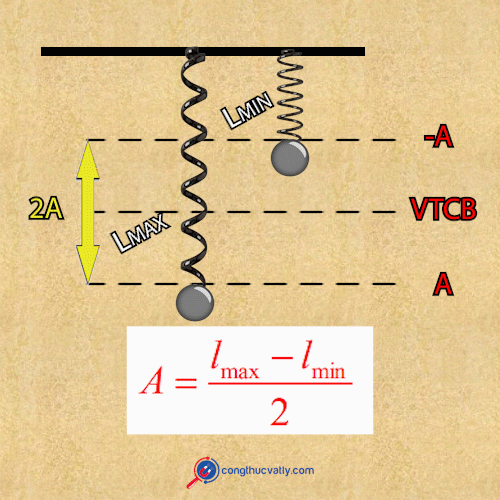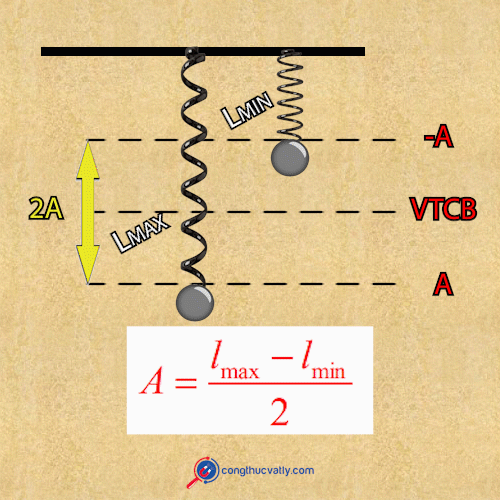
: Biên độ dao động
: Tần số góc ( Tốc độ góc)
: số dao động toàn phần mà chất điểm thực hiện được
: Vận tốc của chất điểm tại vị trí có li độ
: Gia tốc của chất điểm tại vị trí có li độ x
: Vận tốc cực đại của chất điểm
: Gia tốc cực đại của chất điểm
Chứng minh các công thức:
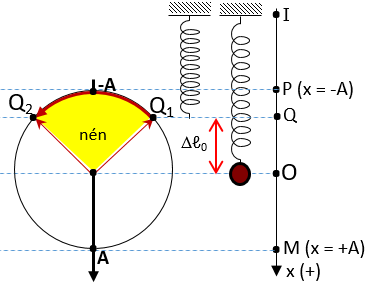
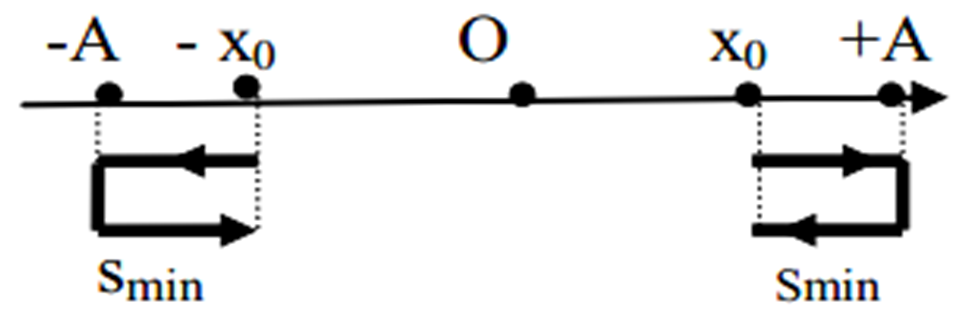
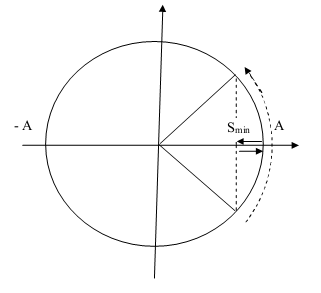
+ Vật chuyển động trên quỹ đạo dài .
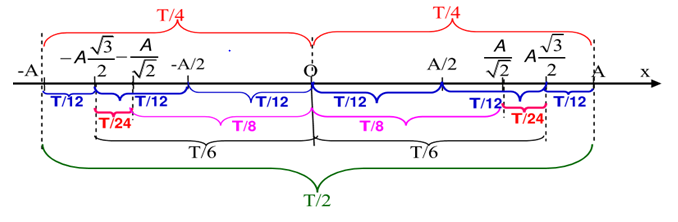
+ Vật chuyển động cứ một vòng sẽ đi được quãng đường là , vật vật đi vòng thì quãng đường sẽ là .
+ Từ công thức tốc độ cực đại của vật: .
+ Từ công thức gia tốc cực đại của vật: .
+ Ta có: và .
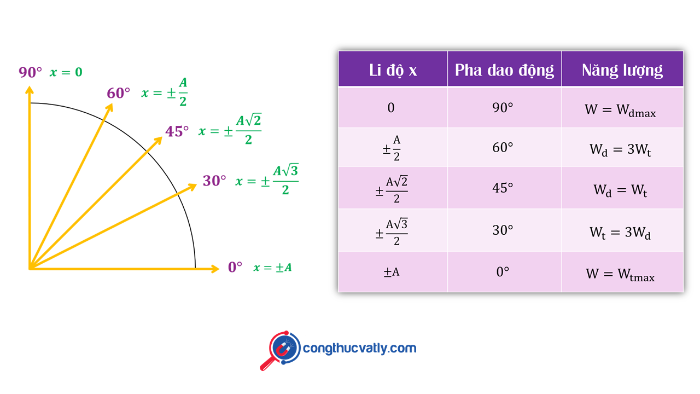
+ Từ hệ thức độc lập thời gian :.
+ Từ hệ thức độc lập thời gian :.