Bài 1: Tổng Quan Về Dao động điều Hòa
1. Biên độ của con lắc lò xo
Chú thích:
: Biên độ dao động
: Chiều dài con lắc lò xo lúc dài nhất
: Chiều dài con lắc lò xo lúc ngắn nhất
2. Độ cứng của lò xo
Chú thích:
: Độ cứng của lò xo (hệ số đàn hồi của lò xo)
: Khối lượng của vật nặng gắn vào con lắc lò xo
: Tần số góc (Tốc độ góc)
Giải thích công thức:
Ta có công thức tính tần số góc của con lắc lò xo: .
3. Hệ thức vuông pha giữa các đại lượng
Chú thích:
: Biên độ dao động .
: Vận tốc của chất điểm tại vị trí có li độ .
: Gia tốc của chất điểm tại vị trí có li độ x .
: Vận tốc cực đại của chất điểm .
: Gia tốc cực đại của chất điểm .
Li độ của chất điểm trong dao động điều hòa .
4. Quãng đường nhỏ nhất trong dao động điều hòa.
Nguyên tắc: Vật đi được quãng đường ngắn nhất khi li độ điểm đầu và điểm cuối có giá trị bằng nhau.
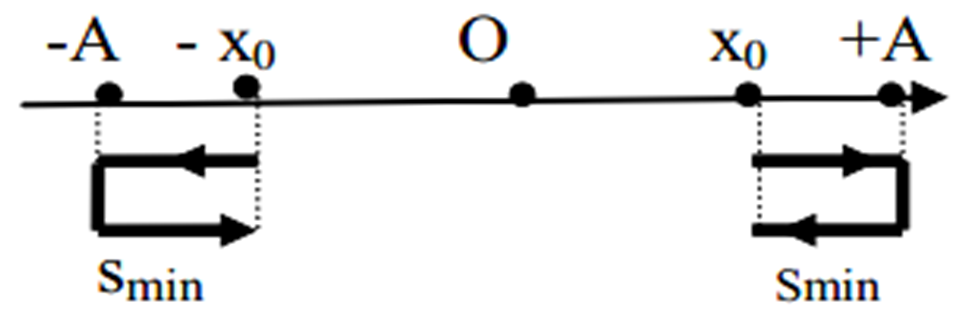
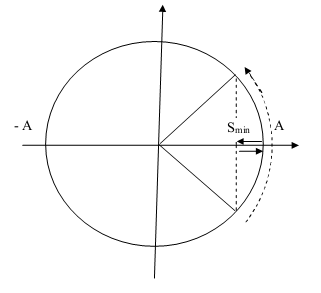
Chú thích:
: Quãng đường nhỏ nhất chất điểm chuyển động trong khoảng thời gian
: Biên độ dao động
: góc quét của chất điểm trong khoảng thời gian
Với: và
Lưu ý:
+ Nếu khoảng thời gian thì tách:. Với :.
+ Công thức còn có thể viết :
Với: .
5. Tốc độ trung bình
Khái niệm:
Tốc độ trung bình là thương số giữa quãng đường chất điểm đi được và thời gian để đi hết được quãng đường đó.
Chú thích:
: Tốc độ trung bình của chất điểm
: Quãng đường chất điểm đi được
: Thời gian mà vật chuyển động được quãng đường
Lưu ý:
+ Tốc độ trung bình của chất điểm trong một chu kỳ: .
+Tốc độ trung bình của chất điểm trong nửa chu kỳ:
6. Vận tốc trung bình
Khái niệm:
Vận tốc trung bình là thương số giữa độ dời của chất điểm và độ biến thiên thời gian.
Chú thích:
: Vận tốc trung bình của chất điểm
: Độ dời của chất điểm
: Thời gian để vật thực hiện độ dời
7. Tốc độ trung bình lớn nhất trong dao động điều hòa
Chú thích:
: Tốc độ trung bình của chất điểm
: Quãng đường lớn nhất chất điểm đi được trong khoảng thời gian
: Thời gian chuyển động của chất điểm
Lưu ý:
với
8. Tốc độ trung bình nhỏ nhất trong dao động điều hòa
Chú thích:
: Tốc độ trung bình của chất điểm
: Quãng đường nhỏ nhất chất điểm đi được trong khoảng thời gian
: Thời gian chuyển động của chất điểm
Lưu ý:
với
9. Lực phục hồi của dao động điều hòa - vật lý 12
Định nghĩa : Lực phục hồi trong dao động điều hòa là tổng hợp các lực làm cho vật dao động điều hòa.Lực phục hồi cũng biến thiên điều hòa cùng tần số với gia tốc .
Công thức :
Chú ý lực phục hồi cùng chiều với gia tốc có độ lớn cực đại tại hai biên bằng 0 tại VTCB
10. Động năng của dao động điều hòa - vật lý 12
Định nghĩa:
Động năng của dao động điều hòa là dạng năng lượng dưới dạng chuyển động .Biến thiên với chu kì và tần số .Trong quá trình chuyển động động năng và thế năng chuyển đổi cho nhau.
Công thức:
Với Động năng của dao động điều hòa
m : Khối lượng của vật
: tần số góc của dao động điều hòa
Biên độ của dao động điều hòa
Chú ý động năng cực đại : tại VTCB và bằng cơ năng
11. Thế năng của dao động điều hòa - vật lý 12
Định nghĩa : Thế năng là dạng năng lượng phụ thuộc vào vị trí .Thế năng biến thiên điều hòa cùng chu kì, tần số với động năng.Thế năng và động năng có thể chuyển hóa cho nhau nhưng cơ năng là một đại lượng bảo toàn.
Công thức:
Chú ý : tại biên và có giá trị bằng cơ năng
12. Năng lượng của vật trong dao động điều hòa - vật lý 12
Định nghĩa : Cơ năng của dao động điều hòa bằng tổng động năng và thế năng.Cơ năng là đại lượng bảo toàn khi bỏ qua ma sát.
Công thức :
13. Thời gian để vật dao động điều hòa có độ lớn vận tốc,động năng không vượt quá - vật lý 12
dùng cho vận tốc.
dùng cho động năng
Thời gian để vật dao động điều hòa có độ lớn vận tốc, động năng không vượt quá u trong 1 chu kì
Công thức
dùng cho vận tốc.
dùng cho động năng
Khi đó vật đi từ vị trí u đến vị trí biên.Các khoảng thời gian này vật đối xứng qua Biên . Khi xét thêm chiều ta lấy khoảng thời gain đó chia cho 2
14. Thời gian để vật dao động điều hòa có độ lớn vận tốc,động năng vượt quá - vật lý 12
dùng cho vận tốc.
dùng cho động năng
Thời gian để vật dao động điều hòa có độ lớn vận tốc, động năng vượt quá u trong 1 chu kì
Công thức
dùng cho vận tốc.
dùng cho động năng
Khi đó vật đi từ vị trí u đến vị trí VTCB.Các khoảng thời gian này vật đối xứng qua VTCB . Khi xét thêm chiều ta lấy khoảng thời gian đó chia cho 2
15. Thời gian để vật dao động điều hòa có độ lớn li độ,lực phục hồi, thế năng vượt quá u- vật lý 12
dùng cho li độ , lực phục hồi . gia tốc.
dùng cho thế năng
Thời gian để vật dao động điều hòa có độ lớn li độ,lực phục hồi, thế năng vượt quá u trong 1 chu kì
Công thức
dùng cho li độ , lực phục hồi . gia tốc.
dùng cho thế năng
Khoảng thời gian này được tính khi vật đi từ vị trí có điều kiện bằng u ra biên.Các khoảng thời gian này đổi xứng nhau qua biên.Khi xét thêm chiều ta lấy khoảng thời gian chia cho 2.
16. Thời gian để vật dao động điều hòa có độ lớn li độ,lực phục hồi, thế năng không vượt quá - vật lý 12
dùng cho li độ , lực phục hồi
dùng cho thế năng
Thời gian để vật dao động điều hòa có độ lớn li độ,lực phục hồi, thế năng không vượt quá u trong 1 chu kì
Công thức
dùng cho li độ , lực phục hồi . gia tốc.
dùng cho thế năng
Khoảng thời gian này được tính khi vật đi từ vị trí có điều kiện bằng u về VTCB.Các khoảng thời gian này đổi xứng nhau qua VTCB.Khi xét thêm chiều ta lấy khoảng thời gian chia cho 2.
17. Li độ, vận tốc của dao động điều hòa sau khoảng thời gian - vật lý 12
Tại thời điểm t1 vật có li độ x1 và vận tốc v1
Đến thời điểm vật có li độ x2 và vận tốc v2
Ta có:
Với , nên
Ta có:
Vậy:
* Đặc biệt:
+ Sau khoảng thời gian (hoặc ) vật trở lại vị trí và chiều chuyển động như cũ: ; .
+ Sau khoảng thời gian [hoặc ] vật qua vị trí đối xứng: ; .
+ Sau khoảng thời gian [hoặc ] vật qua vị trí đối xứng:
18. Các khoảng thời gian liên tiếp đặc biệt - vật lý 12
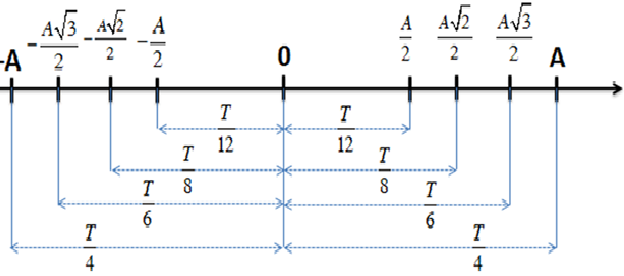
Ví dụ từ :
19. Quãng đường lớn nhất trong dao động điều hòa - vật lý 12
Nguyên tắc: Vật đi được quãng đường dài nhất khi li độ điểm đầu và điểm cuối có giá trị đối nhau.

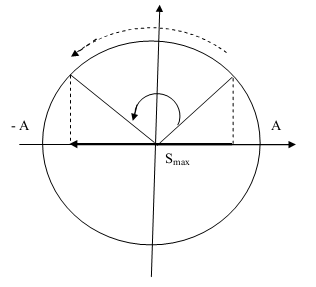
Chú thích:
: Quãng đường lớn nhất chất điểm chuyển động trong khoảng thời gian
: Biên độ dao động
: góc quét của chất điểm trong khoảng thời gian
Với: và
Lưu ý:
+ Nếu khoảng thời gian thì tách:. Với :.
+ Công thức còn có thể viết :
Với: .
20. Mối liên hệ giữa động năng và thế năng - vật lý 12
Chú thích:
: Động năng
: Thế năng
: Số dương bất kỳ
: Li độ của chất điểm
: Biên độ dao động
: Vận tốc của chất điểm tại vị trí có li độ
: Vận tốc cực đại của chất điểm
21. Chu kì của dao động điều hòa - vật lý 12
Khái niệm:
Chu kỳ của dao động điều hòa là khoảng thời gian để vật thực hiện một dao động toàn phần.
Chú thích:
: Chu kỳ dao động .
: Tần số góc (tốc độ góc) .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
Lưu ý:
Thời gian vật đi được tại các vị trí đặc biệt:
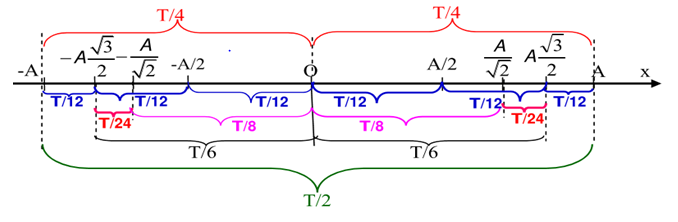
22. Tần số của dao động điều hòa - vật lý 12
Khái niệm:
Tần số của dao động điều hòa là số dao động chất điểm thực hiện được trong một giây.
Chú thích:
: Tần số dao động .
: Tần số góc (tốc độ góc) .
: Chu kỳ dao động của vật .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
23. Vận tốc cực đại của chất điểm trong dao động điều hòa - vật lý 12
Chú thích:
: Tốc độ cực đại của chất điểm
: Tần số góc ( tốc độ góc)
: Biên độ dao động
Lưu ý:
Vận tốc đạt giá trị cực đại khi vật qua vị trí cân bằng theo chiều dương.
Vận tốc đạt giá trị cực tiểu khi vật qua vị trí cân bằng theo chiều âm.
Tốc độ lớn nhất ( xét độ lớn) khi vật ở vị trí cân bằng.
Tốc độ nhỏ nhất (xét độ lớn) khi vật ở hai biên.
24. Gia tốc của chất điểm trong dao động điều hòa - vật lý 12
Công thức:
Từ phương trình .
Chú thích:
: Gia tốc của chất điểm trong dao động điều hòa tại vị trí có li độ
: Tần số góc (tốc độ góc)
: li độ của chất điểm
25. Tốc độ trung bình của chất điểm trong dao động điều hòa - Vật lý 12.
Khái niệm:
Tốc độ của một vật là độ lớn của sự thay đổi vị trí của nó.
Chú thích:
: tốc độ trung bình của chất điểm
: Quãng đường mà chất điểm đi được trong thời gian
: Thời gian vật chuyển động
Lưu ý:
+ Tốc độ trung bình của chất điểm chuyển động trong một chu kỳ :
.
+ Tốc độ trung bình của chất điểm chuyển động trong nửa chu kỳ:
26. Vận tốc trung bình của chất điểm - vật lý 12
Khái niệm:
Vận tốc trung bình trong khoảng thời gian nhất định được định nghĩa là tỉ số giữa sự thay đổi vị trí trong khoảng thời gian đang xét và khoảng thời gian đó.
Chú thích:
: Vận tốc trung bình của chất điểm
: Độ dời của chất điểm
: Vị trí của vật tại thời điểm bắt đầu xét chuyển động
: Vị trí của vật sau khi chuyển động trong thời gian
: Thời gian chuyển động của vật
27. Hệ thức vuông pha giữa các đại lượng - vật lý 12
Li độ và vận tốc vuông pha nhau :
Vận tốc và gia tốc vuông pha nhau:
Chú thích:
: Li độ của chất điểm
: Biên độ dao động
: Tần số góc ( Tốc độ góc)
: Vận tốc của chất điểm tại vị trí có li độ
: Gia tốc của chất điểm tại vị trí có li độ x
: Vận tốc cực đại của chất điểm
: Gia tốc cực đại của chất điểm
Lưu ý: Hai công thức trên còn được gọi là hệ thức độc lập thời gian.
28. Biên độ dao động trong dao động điều hòa - vật lý 12
Chú thích:
: Li độ của chất điểm
: Độ dài quỹ đạo
: Quãng đường vật đi được trong vòng
: Biên độ dao động
: Tần số góc ( Tốc độ góc)
: số dao động toàn phần mà chất điểm thực hiện được
: Vận tốc của chất điểm tại vị trí có li độ
: Gia tốc của chất điểm tại vị trí có li độ x
: Vận tốc cực đại của chất điểm
: Gia tốc cực đại của chất điểm
Chứng minh các công thức:
+ Vật chuyển động trên quỹ đạo dài .
+ Vật chuyển động cứ một vòng sẽ đi được quãng đường là , vật vật đi vòng thì quãng đường sẽ là .
+ Từ công thức tốc độ cực đại của vật: .
+ Từ công thức gia tốc cực đại của vật: .
+ Ta có: và .
+ Từ hệ thức độc lập thời gian :.
+ Từ hệ thức độc lập thời gian :.
29. Phương trình gia tốc trong dao động điều hòa - vật lý 12
Gia tốc là đạo hàm của vận tốc theo thời gian.
.
Chú thích:
: Gia tốc của chất điểm tại thời điểm
: Biên độ dao động (li độ cực đại) của chất điểm
: Tần số góc (tốc độ góc)
: Pha dao động tại thời điểm
: Pha ban đầu của chất điểm tại thời điểm
Thời gian
Liên hệ pha:
Gia tốc sớm pha so với vận tốc Vận tốc chậm (trễ) pha so với gia tốc.
Gia tốc sớm pha so với li độ ( ngược pha ).
Đồ thị:
Đồ thị gia tốc theo thời gian là đường hình sin.
Đồ thị gia tốc theo li độ là một đường thẳng.
Đồ thị gia tốc theo vận tốc là một elip.
30. Phương trình vận tốc trong dao động điều hòa - vật lý 12
Khái niệm:
Vận tốc là đạo hàm của li độ theo thời gian:
Chú thích:
v: Vận tốc của chất điểm tại thời điểm
: Biên độ dao động (li độ cực đại) của chất điểm
: Tần số góc ( tốc độ góc)
: Pha dao động tại thời điểm
: Pha ban đầu của chất điểm tại thời điểm
Thời gian
Đồ thị:
Đồ thị vận tốc theo thời gian là đường hình sin.
Đồ thị vận tốc theo li độ là hình elip.
Liên hệ pha:
Vận tốc sớm pha so với li độ Li độ chậm (trễ) pha so với vận tốc.
Gia tốc sớm pha so với vận tốc Vận tốc chậm (trễ) pha so với gia tốc.
31. Phương trình dao động điều hòa - vật lý 12
Định nghĩa: Hình chiếu của một vật chuyển động tròn đều lên đường kính của nó là một dao động đều hòa.
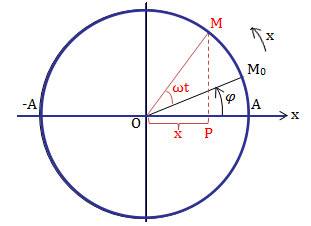
Chú thích:
: Li độ của chất điểm tại thời điểm .
Thời gian .
: Biên độ dao động ( li độ cực đại) của chất điểm .
: Tần số góc (tốc độ góc) .
: Pha dao động tại thời điểm .
: Pha ban đầu của dao động tại thời điểm .
Đồ thị:
Đồ thị của tọa độ theo thời gian là đường hình sin.
32. Tỉ số động năng và thế năng trong dao động điều hòa - vật lý 12
Công thức:
33. Quãng đường của dao động điều hòa trong 1 và 1 nửa chu kì - vật lý 12
Trong 1 chu kì vật đi được 1 dao động , trong nửa chu kì vật đi nửa dao động
Với A: Biên độ
34. Công thức xác định số lần thỏa điều kiện độ lớn trong khoảng thời gian - vật lý 12
Trong 1 chu kì
Số lần vật đi theo chiều âm hoặc chiều dương: 1
Số lần vật đổi chiều trong 1 chu kì : 2
Số lần vật có cùng giá trị : 2
Số lần vật có cùng độ lớn : 4
Số lần vật đi theo chiều âm hoặc chiều dương: 1
Công thức xác định số lần thỏa điều kiện trong khoảng thời gian :
Khi không lấy chiều
:
Tính = ,với góc quét là từ vị trí trí đang xét đến vị trí tiếp
số lần
khi lấy chiều
35. Công thức xác định số lần thỏa điều kiện giá trị trong khoảng thời gian - vật lý 12
Trong 1 chu kì
Số lần vật đi theo chiều âm hoặc chiều dương: 1
Số lần vật đổi chiều trong 1 chu kì : 2
Số lần vật có cùng giá trị : 2
Số lần vật có cùng độ lớn : 4
Số lần vật đi theo chiều âm hoặc chiều dương: 1
Công thức xác định số lần thỏa điều kiện giá trị trong khoảng thời gian :
Không xét chiều
:
Tính = ,với góc quét là từ vị trí trí đang xét đến vị trí tiếp
số lần
Khi ta lấy thêm chiều :
36. Thời điểm vật có li độ x (hoặc v, a, wt, wđ, f) lần thứ n - vật lý 12
- Bước 1: Nhận xét xem trong 1 chu kỳ vật đi qua vị trí x là n0 lần.
- Bước 2: Phân tích
- Bước 3: Tổng thời gian: (Dựa vào vòng tròn để tính )
37. Những thời điểm vật có li độ thỏa điều kiện - vật lý 12
Thời điểm vật có li độ x
38. Những thời điểm vật có gia tốc , lực phục hồi thỏa điều kiện - vật lý 12
Những thời điểm vật có gia tốc , lực phục hồi thỏa điều kiện
39. Những thời điểm vật có vận tốc thỏa điều kiện - vật lý 12
Thời điểm vật có vận tốc v:
40. Quãng đường trong khoảng thời gian xác định -vật lý 12
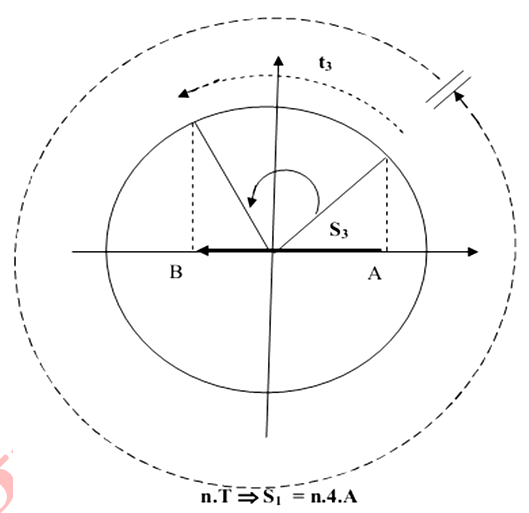
- Bước 1: Tìm
- Bước 2: Lập tỉ số: ; (
- Bước 3: Tìm quãng đường.
- Bước 4: Tìm :
Để tìm được ta tính như sau:
- Tại t = : x =?
- Tại t = ; x =?
Căn cứ vào vị trí và chiều chuyển động của vật tại t1 và t2 để tìm ra S3 (Dựa vào đường tròn)
- Bước 5: thay S3 vào S để tìm ra được quãng đường.
* Chú ý: Các trường hợp đặc biệt:
41. Các vị trí đặc biệt trong dao động điều hòa- vật lý 12
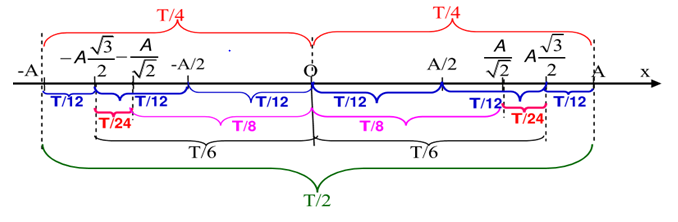
Lưu ý:
Thời gian đi từ 2 biên vào đến các vị trí đặc biệt:
+ Từ biên về vị trí là .
+ Từ biên về vị trí là .
+ Từ biên về vị trí là .
+ Từ biên về vị trí cân bằng là .
42. Thời gian ngắn nhất để thỏa quãng đường s -vật lý 12
Tính góc quay của
43. Vận tốc của chất điểm trong dao động điều hòa - vật lý 12
Từ công thức độc lập thời gian :
Chú thích:
: Li độ của chất điểm
: Biên độ dao động
: Tần số góc ( Tốc độ góc)
: Vận tốc của chất điểm tại vị trí có li độ
44. Tần số góc của dao động điều hòa - vật lý 12
Chú thích:
: Tốc độ góc (Tần số góc) .
: Tần số dao động .
T: Chu kỳ dao động .
: Biên độ dao động .
: Vận tốc của chất điểm tại vị trí có li độ .
: Gia tốc của chất điểm tại vị trí có li độ x .
: Vận tốc cực đại của chất điểm .
: Gia tốc cực đại của chất điểm .
Li độ của chất điểm trong dao động điều hòa .
Chứng minh các công thức:
+ Từ công thức tính tần sô : .
+ Từ công thức tính chu kỳ: .
+ Từ công thức vận tốc cực đại và gia tốc cực đại của chất điểm :
+ Từ công thức độc lập thời gian:
+ Công thức độc lập thời gian tại từng thời điểm là:
45. Xác định pha ban đầu của chất điểm trong dao động điều hòa - vật lý 12
Chú thích:
: Li độ của chất điểm
: Biên độ dao động
: Tần số góc ( Tốc độ góc)
: Vận tốc của chất điểm tại vị trí có li độ
: Pha ban đầu của chất điểm
+ Căn cứ vào thời điểm thì :
Do nên dấu của tùy thuộc vào :
+ Hoặc chia 2 vế phương trình trên :
Lưu ý:
Nếu đề cho tại thì thì :
46. Gia tốc cực đại của chất điểm trong dao động điều hòa -vật lý 12
Chú thích:
: Gia tốc cực đại của chất điểm trong dao động điều hòa
: Tần số góc (tốc độ góc)
A: li độ cực đại của chất điểm (biên độ dao động)
Lưu ý:
Gia tốc đạt giá trị cực đại khi vật ở biên âm.
Gia tốc đạt giá trị cực tiểu khi vật ở biên dương.
Gia tốc đạt độ lớn lớn nhất tại vị trí hai biên.
Gia tốc đạt độ lớn nhỏ nhất tại vị trí cân bằng.
47. Xác định pha của dao động điều hòa - vật lý 12
Chú thích:
: tần số góc của dao động điều hóa
: Pha ban đầu
Bài 2: Con Lắc Lò Xo.
1. Phương trình dao động của con lắc lò xo - vật lý 12
Phương trình dao động của con lắc lò xo:
Vị trí cân bằng là vị trí lò xo không bị biến dạng.Tốc độ góc của phương trình dao động là tốc độ góc của con lắc lò xo
Với Li độ của con lắc lò xo .
Biên độ dao động của con lắc lò xo
Tốc độ góc của con lắc lò xo
Pha ban đầu
Thời điểm
Bước 1: Tính , A
Bước 2: Xác định pha ban đầu
2. Biên độ , tần số góc con lắc lò xo sau va chạm mềm - vật lý 12
Va chạm mềm : con lắc lò xo có va chạm với vật có vận tốc lần lượt .Sau va chạm hai vật bi dính lại và chuyển động cùng vật tốc.
Bảo toàn động lượng :
, là vận tốc sau va chạm
Công thức :
Với x là vị trí so với VTCB mà vật bắt đầu va chạm
3. Chu kì , tần số của con lắc lò xo mắc nối tiếp - vật lý 12
.
Chu kì của lò xo mắc nối tiếp:
Tần số
Chú ý: Khi có n lò xo có cùng độ cứng
suy ra ,
4. Độ cứng của lò xo mắc nối tiếp - vật lý 12
Độ cứng cùa lò xo mắc nối tiếp bằng nghịch đảo tổng nghịch đảo của độ cứng của các lò xo thành phần.
Công thức:
Với : + độ cứng của lò xo khi mắc nối tiếp
+độ cứng của lò xo thành phần
5. Chu kì , tần số của con lắc lò xo mắc song song - vật lý 12
Với : Chu kì con lắc lò xo mắc song song
Tần số lò xo mắc song song
Chú ý: Khi có n lò xo có cùng độ cứng
suy ra ;
6. Công thức tính độ cứng của lò xo mắc song song - vật lý 12
Độ cứng cùa lò xo mắc song song bằng tổng các độ cứng của các lò xo thành phần.
Công thức:
Với : + độ cứng của lò xo khi mắc song song
+độ cứng của lò xo thành phần
7. Chu kì của con lắc lò xo theo thay đổi khối lượng - vật lý 12
Cho hai vật và được gắn lần lượt vào lo xo có độ cứng k thì có chu kì lần lượt là .
Tính chu kì gằn vào lò xo k với
Chu kì mới là
Ví dụ tính chu kì khi thì
8. Độ cứng của lò xo khi bị cắt ngắn - vật lý 12
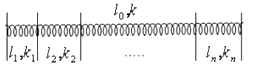
Công thức:
Với là độ cứng của lò xo sau khi cắt
là độ cứng của lò xo ban đầu
là chiều dài ban đầu của lò xo
là chiều dài lúc sau của lò xo
Chú ý: Lò xo càng cắt ngắn độ cứng càng tắng
Có thể áp dụng khí nối thêm lò xo cùng chất liệu.
9. Phương trình gia tốc của con lắc lò xo - vật lý 12
Phương trình gia tốc của con lắc lò xo
Với Biên độ
Tần số góc con lắc lò xo
Gia tốc của vật
Chú ý :
+ Gia tốc chậm pha li độ dài , li độ góc ; chậm pha với vận tốc , cực đại tại VTCB và bằng 0 tại Biên.
+ Với góc nhỏ ta có hệ thức : ,,
10. Phương trình vận tốc của con lắc lò xo - vật lý 12
Phương trình vận tốc của con lắc đơn
Với Li độ
Biên độ
Tần số góc con lắc lò xo
Vận tốc của con lắc lò xo
Chú ý :
+ Vận tốc vuông pha li độ dài và li độ góc, cực đại tại VTCB và bằng 0 tại Biên.
+ Với vận tốc cực đại :
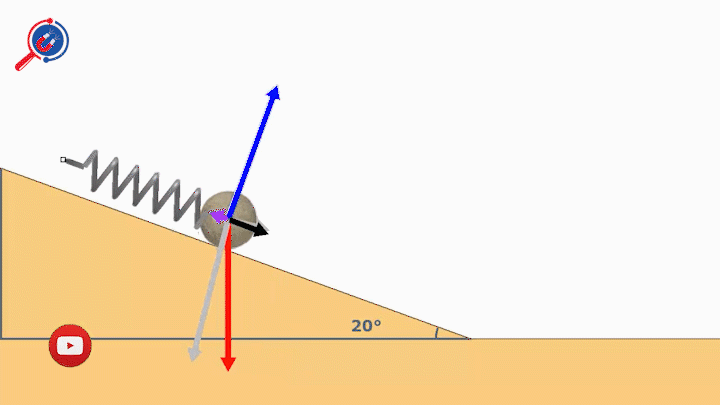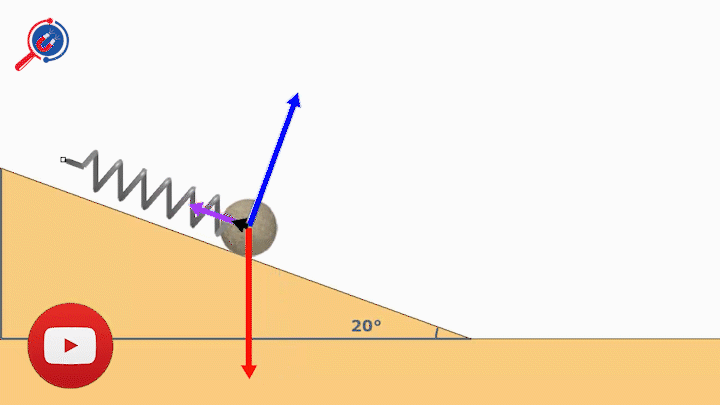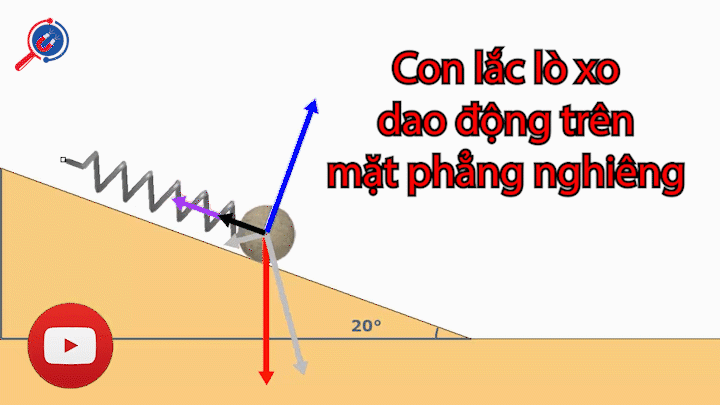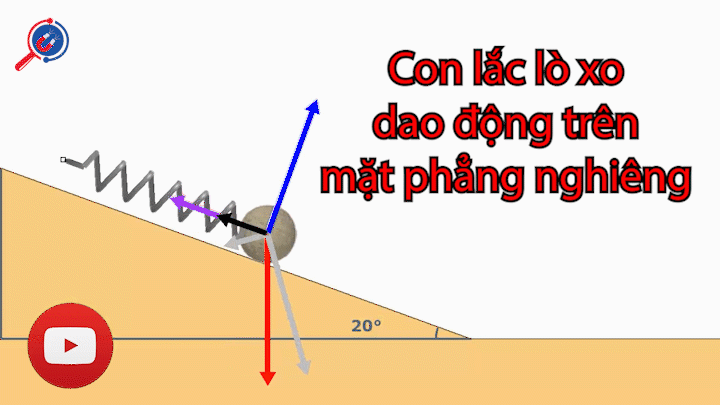
11. Công thức tính chu kì của con lắc lò xo trên mặt phẳng nghiêng - vật lý 12
Công thức
Với T : Chu kì con lắc lò xo trên mặt nghiêng
: Độ biến dạng ban đầu của lò xo
g: Gia tốc trong trường
k : Độ cứng của lò xo
m: Khối lượng của vật
: Góc nghiêng
12. Chiều dài của con lắc lò xo trên mặt nghiêng - vật lý 12

Chú thích:
Độ giãn hoặc nén ban đầu của lò xo
x : Li độ của vật
m: Khối lượng của lò xo
Gia tốc trọng trường
Góc nghiêng của mặt phẳng
Chiều dài của lò xo trong quá trình dao động
A: Biên độ của dao động
k : Độ cứng của lò xo
13. Tốc độ góc quay đều của thanh - vật lý 12
Khi quay ngang:
Khi quay hợp góc :
Khi thanh quay đều:
Khi quay trên phương ngang:
Khi quay hợp với phương thẳng 1 góc :
14. Tần số quay đều của thanh- vật lý 12
Công thức :
Với : tần số quay của thanh .
: tốc độ góc .
N: số vòng
t : thời gian
15. Công thức tính cơ năng của con lắc lò xo - vật lý 12
Định nghĩa : Tổng các dạng năng lượng mà lò xo có được .Cơ năng có giá trị xác định (không biến thiên theo t) và bảo toàn khi bỏ qua ma sát.
Công thức :
Chú ý : Động năng cực đại ở VTCB, cực tiểu ở biên.
Chú thích:
Cơ năng của lò xo
Động năng của lò xo .
Thế năng của lò xo .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dao động cùa lò xo
Độ cứng của lò xo .
Li độ của vật
16. Thế năng của con lắc lò xo - vật lý 12
Định nghĩa : năng lượng mà lò xo có được khi bị biến dạng đàn hồi.Thế năng biến thiên điều hòa theo t với chu kì
Công thức :
Chú ý : Thế năng cực tiểu ở VTCB, cực đại ở biên.
Chú thích:
Thế năng của lò xo .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dao động cùa lò xo
Độ cứng của lò xo .
Pha ban đầu của dao động
Li độ của vật
17. Động năng của con lắc lò xo - vật lý 12
Định nghĩa : năng lượng mà lò xo có được dưới dạng chuyển động.Động năng biến thiên điều hòa theo t với chu kì
Công thức :
Chú ý : Động năng cực đại ở VTCB, cực tiểu ở biên.
Chú thích:
Động năng của lò xo .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dao động cùa lò xo
Độ cứng của lò xo .
Li độ của vật
18. Vận tốc của con lắc lò xo - vật lý 12
Chú thích :
Vận tốc của con lắc lò xo
: Tần số góc của con lắc lò xo
Vận tốc cực đại
: Động năng của con lắc lò xo
n : Tỉ số động năng và thế năng
x : li độ của vật
A: Biên độ của vật
19. Tần số góc của con lắc lò xo - vật lý 12
Chú thích:
: Tốc độ góc (Tần số góc) .
: Tần số dao động .
T: Chu kỳ dao động .
Khối lượng của vật treo
: Độ cứng của lò xo
: Độ dãn của lò xo tại vị trí cân bằng
: Gia tốc trọng trường
20. Chiều dài cân bằng của con lắc lò xo - vật lý 12
Chú thích:
: Chiều dài lớn nhất mà lò xo đạt được khi thực hiện dao động điều hòa .
: Chiều dài lò xo khi gắn vật và chưa dao động .
: Chiều dài ngắn nhất mà lò xo đạt được khi thực hiện dao động điều hòa .
Chứng minh công thức:
+Từ
Cộng vế theo vế ta được
21. Công thức tính thời gian chuyển động của con lắc lò xo - vật lý 12
Công thức:
Với : Khoảng thời gian .
: Góc quay
: Tốc độ góc của con lắc lò xo .
max giữa lần liên tiếp khi hai vị trí đối nhau qua biên.
min giữa lần liên tiếp khi hai vị trí đối nhau qua VTCB
Khi ở bài tập liên quan đến các loại năng lượng ta nên chuyển về li độ và tìm.
22. Li độ của vật trong con lắc lò xo - vật lý 12
Chú thích : Li độ của vật
: Biên độ của vật
Gia tốc cực đại
:Gia tốc của vật
n : tỉ số động năng và thế năng
Vận tốc của vật
: Vận tốc cực đại của vật
l: Chiều dài dây đang bị thay đổi
: Chiều dài ban đầu
:Độ biến dạng của lò xo tại VTCB
23. Lực đàn hồi của con lắc lò xo - vật lý 12
Khi lò xo nằm ngang :
cực đại tại hai biên và cực tiểu tại vị trí cân bằng
Khi lò xo treo thẳng đứng :
Trường hợp 1 :
max = tại biên dưới
min tại vị trí không biến dạng
Tại biên trên :
Trường hợp 2:
tại biên dưới
24. Độ biến dạng tại VTCB của lò xo - vật lý 12
Chú thích:
: Độ biến dạng (độ dãn hay nén) của lò xo tại vị trí cân bằng .
: Chiều dài lò xo khi gắn vật và chưa dao động .
: Chiều dài tự nhiên (chiều dài ban đầu) của lò xo
m: khối lượng của vật
Gia tốc trọng trường
Độ cứng của lò xo
25. Chu kỳ của con lắc lò xo - vật lý 12
Khái niệm:
Chu kỳ của lắc lò xo dao động điều hòa là khoảng thời gian vật thực hiện được một dao động toàn phần.
Chú thích:
: Chu kỳ dao động .
: Tần số góc (tốc độ góc) .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
: Khối lượng vật treo trên lò xo .
: Độ cứng của lò xo .
: Gia tốc trọng trường .
: Độ biến dạng của lò xo tại vị trí cân bằng .
Lưu ý:
Ta có :
26. Lực phục hồi của con lắc lò xo- vật lý 12
Định nghĩa: Lực phục hồi là lực hoặc hợp lực làm cho vật dao động điều hòa.
Công thức:
Chú thích:
Lực phục hồi
Tần số góc của dao động
Li độ của vật
+Lực hồi phục cực đại tại biên , cực tiểu tại VTCB
+Lực hồi phục cùng chiều với gia tốc
Đối với con lắc lò xo nằm ngang : lực hồi phục cũng chính là lực đàn hồi
27. Lực đàn hồi cực đại và cực tiểu của lò xo thẳng đứng độ dãn đầu nhỏ hơn A - vật lý 12
Chú thích :
Lực đàn hồi max tại biên dương và cực tiểu tại vị trí không biến dạng
28. Lực đàn hồi cực đại và cực tiểu của lò xo thẳng đứng độ dãn đầu lớn hơn A - vật lý 12
Chú thích : Khi lò xo có , trong quá trình DĐĐH lò xo luôn dãn.
Lực đàn hồi max tại biên dương và cực tiểu tại vị trí biên âm
29. Thời gian nén và dãn của lò xo trong một chu kỳ khi A >độ dãn đầu - vật lý 12
Khi con lắc lò xo treo thẳng đứng có .Thì lò xo có thể bị dãn hoăc nén
Lò xo bị dãn khi đi từ về VTCB ra biên + và ngược lại
Lò xo bị nén khi đi từ ra biên - và ngược lại
Với Thời gian lò xo dãn trong 1 chu kỳ
: Thời gian lò xo nén trong 1 chu kỳ
: Chu kỳ dao động của con lắc lò xo
Độ biến dạng tại VTCB
Biên độ của dao động
30. Thời gian nén và dãn của lò xo trong một chu kỳ khi A < độ dãn đầu - vật lý 12
Khi con lắc lò xo treo thẳng đứng có .Thì lò xo luôn bị dãn.
Với Thời gian lò xo dãn trong 1 chu kỳ
: Thời gian lò xo nén trong 1 chu kỳ
: Chu kỳ dao động của con lắc lò xo
31. Quãng đường của con lắc lò xo trong một khoảng thời gian - vật lý 12
Ta lấy tỉ số :
Với n là số tự nhiên dương ví dụ : 1,3,5,6,7,8,14,...
m là số bán nguyên ví dụ : 0,5 ; 1,5
q là phần dư nhỏ hơn 0,5
Quãng đường vật đi :
Tính s :
+
+
Khi hướng về biên
Khi ;
Khi ;
Khi hướng về vị trí cân bằng:
32. Chu kì của con lắc lò xo theo độ tăng , giảm khối lượng - vật lý 12
;
Với Chu ki con lắc lúc sau
Chu kì con lắc ban đầu
Khối lượng ban đầu
: Độ tăng giảm khối lượng
33. Biên độ dao động của con lắc lò xo- vật lý 12
Chú thích:
: Chiều dài ngắn nhất mà lò xo đạt được khi thực hiện dao động điều hòa .
: Chiều dài lớn nhất mà lò xo đạt được khi thực hiện dao động điều hòa .
: Biên độ dao động của con lắc lò xo
L: Chiều dài quỹ đạo của con lắc lò xo
S: quãng đường vật đi trong 1 chi kì
Chứng minh công thức:
+ Từ
Cộng vế theo vế ta được
34. Tần số dao động của con lắc lò xo - vật lý 12
Khái niệm:
Tần số dao động là số dao động và chất điểm thực hiện được trong một giây.
Chú thích:
: Tần số dao động .
: Tần số góc (tốc độ góc) .
: Chu kỳ dao động của vật .
: Số dao động mà chất điểm thực hiện được trong khoảng thời gian .
Thời gian thực hiện hết số dao động .
35. Biên độ , tần số góc con lắc lò xo sau va chạm đàn hồi - vật lý 12
Va chạm đàn hồi : con lắc lò xo có va chạm với vật có vận tốc lần lượt
Bảo toàn động lượng :
Bảo toàn cơ năng :
Công thức :
Với x là vị trí so với VTCB mà vật bắt đầu va chạm
36. Nhiệt lượng tòa ra của va chạm mềm - vật lý 12
Công thức:
Với : Nhiệt lượng tòa ra
Vận tốc sau va chạm mềm
Khối lượng của vật
Vận tốc ban đầu của vật
37. Chiều dài ngắn nhất của lò xo - vật lý 12
=
Chiều dài con lắc lò xo ngắn nhất khi vật đạt đến vị trí biên trên khi dao động điều hòa.
Chú thích :
: Chiều dài ngắn nhất mà lò xo đạt được khi thực hiện dao động điều hòa .
: Chiều dài lò xo khi gắn vật và chưa dao động .
: Biên độ dao động của con lắc lò xo .
Độ nén ban đầu rồi thả của lò xo
38. Chiều dài lớn nhất của lò xo - vật lý 12
Chiều dài con lắc lò xo lớn nhất khi vật đạt đến vị trí biên dưới khi dao động điều hòa.
Chú thích :
: Chiều dài lớn nhất mà lò xo đạt được khi thực hiện dao động điều hòa .
: Chiều dài lò xo khi gắn vật và chưa dao động .
: Biên độ dao động của con lắc lò xo .
Độ dãn khi kéo ra rồi thả của lò xo
Bài 3: Con Lắc đơn.
1. Công thức tính độ biến thiên chu kì khi l, g, t thay đổi rất nhỏ - vật lý 12
Khi cả l và g đều thay đổi một lượng rất nhỏ thì:
Khi cả nhiệt độ và g thay đổi một lượng rất nhỏ thì:
2. Biên độ dài con lắc đơn sau va chạm - vật lý 12
Va chạm mềm: là sau va chạm hai vật dính chặt vào nhau
Áp dụng định luật bảo toàn động lượng:
VTCB không đổi giả sử va chạm tại li độ x:
Biên độ sau va chạm :
,V vận tốc sau va chạm
3. Công thức tính độ biến thiên chu kì của con lắc thay đổi do độ cao , độ sâu- vật lý 12
Khi đưa từ độ cao lên :
Đưa lên cao: , đưa xuống .Khi vị trí ban đầu ở mặt đất
Khi đưa từ độ sâu lên :
Đưa xuống sâu: , đưa lên .Khi vị trí ban đầu ở mặt đất
4. Công thức tính chu kì của con lắc vướng đinh - vật lý 12
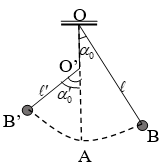
Gọi chiều dài dây treo như hình:
Dao động của con lắc gồm hai giai đoạn:
+ Nửa dao động với chu kì
+ Nửa dao động với chu kì
Chu kì dao động của con lắc
; với là chukì con lắc vướng đinh
5. Công thức tính lực căng dây của con lắc đơn - vật lý 12
Khi con lắc ở vị trí li độ góc :
Công thức
Khi góc nhỏ:
Khi vật ở biên: hay
Khi ở VTCB: hay
Chú thích :
: Lực căng dây
m: Khối lượng con lắc
g: Gia tốc trọng trường
Li độ góc
: Biên độ góc
6. Công thức tính biên độ dài và biên độ góc sau khi vướng đinh - vật lý 12
Gọi là biên độ góc cực đại ứng với chiều dài dây là ;
là biên độ góc cực đại ứng với chiều dài dây là
Gọi là biên độ dài cực đại ứng với chiều dài dây là ;
là biên độ dài cực đại ứng với chiều dài dây là
Công thức :
;
Chứng minh :
7. Công thức tính độ biến thiên chu kì con lắc đơn do nhiệt độ - vật lý 12
Khi nhiệt độ thay đổi từ đến :
Công thức
Với là hệ số nở dài
Khoảng thời gian nhanh, chậm :
8. Công thức tính độ biến thiên chu kì theo nhiệt độ và độ cao - vật lý 12
+ Khi đưa con lắc ở mặt đất (nhiệt độ ) lên độ cao (nhiệt độ ):
Với Chu kì chạy đúng
độ sai lệch
hệ số nở dài
h: độ cao
: Bán kính Trái đất
9. Công thức tính lực phục hồi của con lắc đơn - vật lý 12
Lực hồi phục của con lắc đơn là hợp lực của lực căng dây và trọng lực giúp con lắc đơn dao động điều hòa.
Công thức:
Tại biên lực phục hồi cực đại
Tại VTCB lực phục hồi bằng 0
Chú thích:
: Lực phục hồi của con lắc đơn
Li độ góc
Li độ dài
Tốc độ góc của dao động con lắc đơn
10. Lực căng dây cực tiểu của con lắc đơn - vật lý 12
hay
Khi vật ở Biên: hay
Chú thích :
: Lực căng dây
m: Khối lượng con lắc
g: Gia tốc trọng trường
Li độ góc
: Biên độ góc
11. Lực căng dây cực đại của con lắc đơn - vật lý 12
hay
Khi ở VTCB: hay
Chú thích :
: Lực căng dây
m: Khối lượng con lắc
g: Gia tốc trọng trường
Li độ góc
: Biên độ góc
12. Tỉ số động năng và thế năng con lắc đơn - vật lý 12
Công thức :
13. Động năng của con lắc đơn - vật lý 12
Định nghĩa : năng lượng mà con lắc có được dưới dạng chuyển động.Động năng biến thiên điều hòa theo t với chu kì
Công thức :
Chú ý : Động năng cực đại ở VTCB, cực tiểu ở biên.
Chú thích:
Động năng của con lắc đơn .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dài của dao động con lắc
Độ cứng của lò xo .
Li độ dài của dao động con lắc
Pha ban đầu
14. Thế năng của con lắc đơn - vật lý 12.
Định nghĩa : năng lượng mà con lắc có được do được đặt trong trọng trường.Thế năng biến thiên điều hòa theo t với chu kì
Công thức :
Chú ý : Thế năng cực đại ở biên, cực tiểu ở VTCB.
Chú thích:
Thế năng của con lắc đơn .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dài của dao động con lắc
Độ cứng của lò xo .
Li độ dài của dao động con lắc
Pha ban đầu
15. Cơ năng của con lắc đơn - vật lý 12
Định nghĩa : Tổng các dạng năng lượng mà con lắc có được .Cơ năng có giá trị xác định (không biến thiên theo t) và bảo toàn khi bỏ qua ma sát.
Công thức :
Chú ý : Động năng cực đại ở VTCB, cực tiểu ở biên.
Chú thích:
Cơ năng của con lắc đơn
Động năng của con lắc đơn .
Thế năng của con lắc đơn .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dài của dao động con lắc
Tốc độ góc của con lắc .
Biên độ dài của dao động con lắc
Chiều dài dây treo
g: gia tốc trọng trường
16. Phương trình li độ dài , li độ góc của con lắc đơn - vật lý 12
Phương trình li độ dài , li độ góc của con lắc đơn
Với Li độ dài
Biên độ dài
Li độ góc
Biên độ góc
Tần số góc con lắc đơn
Chú ý :
+ Li độ dài , li độ góc cùng pha cực đại tại biên và bằng 0 tại VTCB.
+ Với góc nhỏ ta có hệ thức :
17. Điều kiện của đõng hồ chạy đúng do nhiệt độ và độ cao - vật lý 12
Điều kiện để đồng hồ chạy đúng:
18. Thời gian ngắn nhất để vật thỏa yêu cầu bài toán - vật lý 12
Thời gian ngắn nhất để vật thỏa yêu cầu bài toán
Bước 1 : Xác định vị trí ban đầu xét.
Bước 2 : Xác định vị trí lần đầu vật thỏa yêu cầu bài toán
Bước 3 : Tính góc quay suy ra , Với là góc quay
Hoặc dùng VTLG:
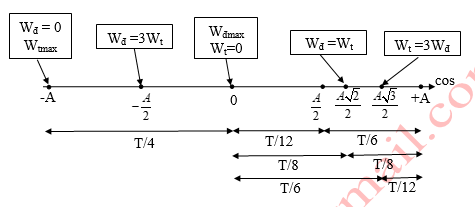
19. Công thức tính vận tốc của con lắc đơn - vật lý 12
;
Công thức:
hay
+ tại VTCB
+ tại 2 biên
Với góc nhỏ :
Hoặc
Chú thích:
Vận tốc của con lắc .
Gia tốc trọng trường .
Chiều dài dây .
Li độ góc
Biên độ góc
20. Công thức xác định chu kì của con lắc đơn trong dao động điều hòa.
Chú thích:
: chu kì dao động
: chiều dài dây treo
gia tốc trọng trường
21. Phương trình vận tốc của con lắc đơn - vật lý 12
Phương trình vận tốc của con lắc đơn
Với Li độ dài
Biên độ dài
Li độ góc
Biên độ góc
Tần số góc con lắc đơn
Vận tốc của con lắc đơn
Chú ý :
+ Vận tốc vuông pha li độ dài và li độ góc, cực đại tại VTCB và bằng 0 tại Biên.
+ Với vận tốc cực đại :
22. Phương trình gia tốc của con lắc đơn - vật lý 12
Phương trình gia tốc của con lắc đơn
Với Biên độ dài
Li độ góc
Biên độ góc
Tần số góc con lắc đơn
Gia tốc của vật
Chú ý :
+ Gia tốc chậm pha li độ dài , li độ góc ; chậm pha với vận tốc , cực đại tại VTCB và bằng 0 tại Biên.
+ Với góc nhỏ ta có hệ thức : ,,
23. Công thức chu kì của con lắc thay đổi do lực Acimet -vật lý 12
Lực đẩy Acsimet :
là khối lượng riêng của môi trường vật dao động , V là thể tích vật chiếm chỗ .
Với
Khi :
Khi :
Chu kì mới :
24. Công thức tính chu kì của con lắc thay đổi bởi lực tác dụng , lực quán tính - vật lý 12
Lực tác dụng :
Lực quán tính:
Khi lực cùng chiều với trọng lực:
Lực tác dụng : Ví dụ vật bị tác dụng hướng xuống
Lực quán tính: Ví dụ thang máy đi xuống nhanh dần đều, đi lên chậm dần đều với gia tốc a
Khi lực ngược chiều với trọng lực:
Lực tác dụng : Ví dụ vật bị tác dụng hướng lên
Lực quán tính: Ví dụ thang máy đi lên nhanh dần đều ,đi xuống chậm dần đều với gia tốc a
Khi lực vuông với trọng lực:
Khi lên dốc là góc mặt phẳng nghiêng
Chu kì mới :
25. Chu kì của lắc đơn bị thay đổi do điện trường theo phương xiên - vật lý 12
Lực điện :
Với : Cường độ điện trường
Hiệu điện thế
Khoảng cách
Khi :
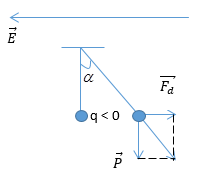
; , là góc lệch theo phương đứng
Khi
Chu kì mới :
26. Chu kì của lắc đơn bị thay đổi do điện trường thẳng đứng - vật lý 12
Lực điện :
Với : Cường độ điện trường
Hiệu điện thế
Khoảng cách
Khi : cùng phương , cùng chiều
Áp dụng khi :;
Khi : cùng phương , ngược chiều
Áp dụng khi
Chu kì mới :
27. Công thức tính thời gian nhanh chậm trong thời gian t - vật lý 12
Khi :đồng hồ chạy chậm lại.
Khi : đồng hồ chạy nhanh lên
Thời gian chạy nhanh hay chậm trong t:
Với : Thời gian đồng hồ chạy nhanh hay chậm trong t
Thời gian
Độ biến thiên chu kì
Chu kì con lắc chạy đúng
28. Công thức độ biến thiên chu kì do gia tốc hấp dẫn- vật lý 12
Với Chu kì con lắc trên thiên thể
Chu kì con lắc trên trái đất
Bán kính thiên thể
: bán kính trái đất
Khối lượng thiên thể
:Khối lượng trái đất
29. Công thức liên hệ giữa li độ dài và li độ góc - vật lý 12
Công thức:
Chú thích :
Li độ dài của con lắc đơn
Chiều dài dây treo
Li độ góc của con lắc đơn
30. Công thức tính gia tốc của con lắc đơn - vật lý 12
Gia tốc tiếp tuyến : gia tốc tiếp tuyến có phương tiếp tuyến với quỹ đạo dao động con lắc đơn
+ Công thức :
cực đại tại VTCB , cực tiểu tại biên
Gia tốc pháp tuyến :gia tốc tiếp tuyến có phương vuông tiếp tuyến với quỹ đạo dao động con lắc đơn
+ Công thức :
Gia tốc toàn phần : Tổng hợp vecto gia tốc tiếp tuyến và gia tốc pháp tuyến.
31. Công thức tính chu kì con lắc đơn theo hai chiều dài - vật lý 12
- Chu kì dao động của con lắc đơn có chiều dài và lần lượt là và thì:
Chu kì con lắc có chiều dài là
Chu kì con lắc cò chiều dài , là
Chu kì con lắc cò chiều dài , là
32. Hệ thức vuông pha cho con lắc đơn- vật lý 12
Công thức độc lập với thời gian
Bài 4: Các Loại Dao động.
1. Công thức tính quãng đường đến khi dừng - vật lý 12
Công thức :
Với S : Quãng đường vật đi được đến khi dừng
Biên độ dao động
Độ cứng của lò xo
Lực cản
Chứng minh :
2. Công thức tính độ giảm biên độ của dao động tắt dần - vật lý 12
- Độ giảm biên độ sau một dao động:
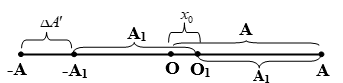
với là lực cản
Nếu FC là lực ma sát thì
Nếu vật chuyển động theo phương ngang:
3. Công thức tính số dao động , thời gian dừng của dao động tắt đần - vật lý 12
- Số dao động thực hiện được: :
Nếu là lực ma sát :
Thời gian đến lúc dừng: ,với T là chu kì dao động
4. Công thức tính số lần qua VTCB của vật dao động tắt dần - vật lý 12
Số lần qua VTCB của vật
+ khi (n là số nguyên) thì số lần qua VTCB sẽ là 2n.
+ khi thì số lần qua VTCB của vật là 2n+1.
+ khi thì số lần qua VTCB của vật là 2n+2.
5. Công thức tính vận tốc của vật khi vật đi được quãng đường S - vật lý 12
Chứng minh :
Với v: vận tốc của vật
Biên độ của dao động
x: Li độ của vật
Lực ma sát
Quãng đường vật đã đi
m : Khối lượng của vật
6. Công thức tính biên độ cuối của dao động tắt dần - vật lý 12
Lập tỉ số
k=
Biên độ cuối :
7. Công thức tính năng lượng cần cung cấp cho mỗi chu kì của dao động duy trì - vật lý 12
Công thức :
Độ giảm năng lượng của dao động sau 1 chu kì :
Sau N chu kì
Năng lượng cần cung cấp sau N chu kì :
Công suất cung cấp năng lượng:
8. Độ giảm cơ năng của dao động tắt dần - vật lý 12
Công thức :
Với Độ giảm cơ năng
Biên độ lúc sau
: Biên độ ban đầu
Cơ năng ban đầu
9. Công thức tính vận tốc qua vị trí cân bằng của dao động tắc dần - vật lý 12
Công thức
Với độ giảm biên độ chu kì , n số lần qua VTCB
Vận tốc cực đại qua VTCB lần đầu:
10. Dao động tự do - vật lý 12
Dao động tự do
Dao động tự do là dao động mà chu kì và tần số của hệ chỉ phục thuộc vào cấu tạo của hệ mà không phụ thuộc vào các yếu tố bên ngoài.
Ví dụ :
Chu kì của con lắc lò xo :
Chu kì của con lắc đơn :
11. Điều kiện xảy ra cộng hưởng - vật lý 12
- Khi vật dao động cưỡng bức thì tần số (chu kì) dao động của vật bằng với tần số (chu kì) của ngoại lực:
và khi đó max
+Hiện tượng cộng hưởng chỉ xảy ra với dao động cưỡng bức
+Biên độ dao động cưỡng bức phụ thuộc vào ma sát của môi trường.
12. Công thức tính vận tốc của xe để con lắc trên xe cộng hưởng - vật lý 12
Vận tốc của xe để con lắc đặt trên xe có cộng hưởng (biên độ dao động cực đại):
Chu kì kích thích trong đó L là khoảng cách ngắn nhất giữa hai mối ray tàu hỏa hoặc hai ổ gà trên đường…
Công thức :
với hay
13. Dao động cưỡng bức - vật lý 12
Dao động cưỡng bức là dao động của hệ chịu tác dụng của ngoại lực biến thiên tuần hoàn:
Dao động cưỡng bức là dao động của hệ chịu tác dụng của ngoại lực biến thiên tuần hoàn:
Hệ có đặc diểm :
Biên độ hệ dao động phụ thuộc vào ; là chu kì riêng của hệ dao động ; tỉ lệ với biên độ ngoại lực
Khi thì A càng lớn ; xảy ra cộng hưởng A lớn nhất .A phụ thuộc vào ma sát của môi trường
14. Dao động tắt dần ,dao động duy trì - vật lý 12
Dao động tắt dần ,dao động duy trì
Dao động tắt dần là dao động có giảm dần ; không đổi . Ma sát càng lớn vật càng nhanh tắc dần.
Dao động duy trì là dao động tắt dần mà ta cung cấp cho hệ một phần năng lượng mà vật mất đi do ma sát mỗi chu kì .Ví dụ : con lắc đồng hồ
Bài 5: Tổng Hợp Dao động điều Hòa.
1. Phương trình tổng hợp dao động điều hòa -vật lý 12
Cho hai dao động điều hòa cùng tần số :
Với x : Phương trình dao động tổng hợp .
:Biên độ của dao động 1, 2, tổng hợp.
: Pha ban đầu của dao động 1, 2, tổng hợp.
Trong đó
2. Công thức tính biên độ và pha ban đầu dao động tổng hợp- vật lý 12
Công thức:
Cách 1:Dùng công thức
Tính A:
Tính pha ban đầu
Với :Biên độ dao động thành phần
Cách 2: Dùng máy tính :
Bước 1: Bấm MODE 2 để sang dạng cmplx
Bước 2:Chuyển sang radian bằng cach1 nhấn shift mode 4
Bước 3: Biễu diễn Nhập SHIFT (-) + Nhập SHIFT (-)
Bước 4:
+ Nhấn SHIFT 2 3 = hiển thị kết quả
+ Sau đó nhấn SHIFT + = hiển thị kết quả là . Nhấn SHIFT = hiển thị kết quả là .
Lưu ý: Chế độ hiển thị màn hình kết quả:
Sau khi nhập ta nhấn dấu = có thể hiển thị kết quả dưới dạng số vô tỉ, muốn kết quả dưới dạng thập phân ta nhấn SHIFT = (hoặc nhấn phím ) để chuyển đổi kết quả hiển thị.
3. Công thức tính biên độ , pha dao động tổng hợp ở các trường hợp đặc biệt- vật lý 12
+Khi : Hai dao động cùng pha
+Khi : Hai dao động ngược pha có pha ban đầu của dao động biên độ lớn hơn Ví dụ
+Khi :Hai dao động vuông pha
+Khi và ;
4. Công thức tính dao động thành phần -vật lý 12
Ta có dao động cần tìm :
Cách 1: Dùng công thức:
Tính :
Tính pha ban đầu
Với :Biên độ dao động thành phần
Cách 2: Dùng máy tính :
Bước 1: Bấm MODE 2 để sang dạng cmplx
Bước 2:Chuyển sang radian bằng cach1 nhấn shift mode 4
Bước 3: Biễu diễn Nhập SHIFT (-) - Nhập SHIFT (-)
Bước 4:
+ Nhấn SHIFT 2 3 = hiển thị kết quả
+ Sau đó nhấn SHIFT + = hiển thị kết quả là . Nhấn SHIFT = hiển thị kết quả là .
Lưu ý: Chế độ hiển thị màn hình kết quả:
Sau khi nhập ta nhấn dấu = có thể hiển thị kết quả dưới dạng số vô tỉ, muốn kết quả dưới dạng thập phân ta nhấn SHIFT = (hoặc nhấn phím ) để chuyển đổi kết quả hiển thị.
* Lưu ý:
- Đối với bài toán tổng hợp dao động điều hòa mà đề bài có nhắc đến thay đổi biên độ của dao động này để biên độ của dao động khác đạt giá trị cực đại (hoặc cực tiểu) thì ta phải vẽ giản đồ vecto và dùng định lý hàm sin để giải.
5. Công thức tính khoảng cách giữa hai chất điểm dao động điều hòa -vật lý 12
Trên cùng 1 trục tọa độ Ox:Hai dao động cùng tần số (không va chạm nhau)
Công thức
Bấm máy
Hoặc dùng định lý hàm cos tìm được khoảng cách lớn nhất:
Bài 6: Con Lắc Gặp Nhau.
1. Công thức tính thời gian giữa hai lần trùng phùng - vật lý 12
Để xác định chu kỳ của một con lắc lò xo (con lắc đơn) người ta so sánh với chu kỳ (đã biết) của một con lắc khác .
Hai con lắc gọi là trùng phùng khi chúng đồng thời đi qua một vị trí xác định theo cùng một chiều.
Gọi thời gian giữa hai lần trùng phùng liên tiếp là . Ta có:
(với và là số dao động con lắc 1 và 2 thực hiện trong thời gian )
Ta chứng minh được thời gian giữa hai lần trùng phùng là:
* Lưu ý: Công thức trên chỉ đúng cho con lắc trùng phùng; còn nếu đề bài cho không thỏa mãn điều kiện trên thì ta dùng công thức: 2 con lắc gặp nhau khi ở cùng vị trí: x1 = x2 từ đó giải ra thời gian .