Khái niệm:
là độ lệch pha của điểm đang xét so với hai nguồn phát sóng. Do có hai nguồn sóng nên mỗi nguồn gây cho tại vị trí M một độ lệch pha tương ứng.
Đơn vị tính: Radian (Rad)
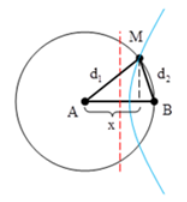
Khái niệm:
là độ lệch pha của điểm đang xét so với hai nguồn phát sóng. Do có hai nguồn sóng nên mỗi nguồn gây cho tại vị trí M một độ lệch pha tương ứng.
Đơn vị tính: Radian (Rad)

Chia sẻ qua facebook
Hoặc chia sẻ link trực tiếp:
congthucvatly.com/bien-so-do-lech-pha-tai-mot-diem-voi-moi-nguon-song-vat-ly-12-428
Khái niệm:
là độ lệch pha của điểm đang xét so với hai nguồn phát sóng. Do có hai nguồn sóng nên mỗi nguồn gây cho tại vị trí M một độ lệch pha tương ứng.
Đơn vị tính: Radian (Rad)

Khái niệm:
là khoảng cách từ các điểm đang xét đến nguồn phát sóng .
Đơn vị tính: centimét
Khái niệm:
là độ lệch pha của điểm đang xét so với hai nguồn phát sóng. Do có hai nguồn sóng nên mỗi nguồn gây cho tại vị trí M một độ lệch pha tương ứng.
Đơn vị tính: Radian (Rad)

Khái niệm:
là khoảng cách từ các điểm đang xét đến nguồn phát sóng .
Đơn vị tính: centimét

Khái niệm:
là độ lệch pha của điểm đang xét so với hai nguồn phát sóng. Do có hai nguồn sóng nên mỗi nguồn gây cho tại vị trí M một độ lệch pha tương ứng.
Đơn vị tính: Radian (Rad)

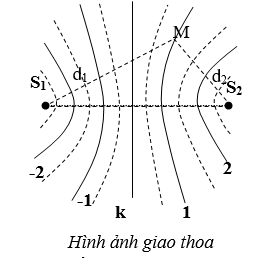
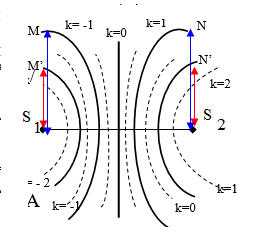
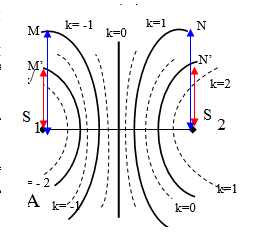
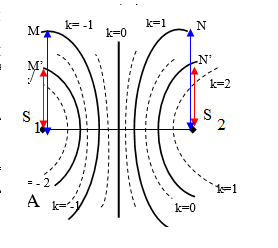
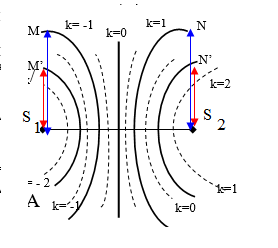
;Khoảng cách từ M đến 2 nguồn
Khi hai nguồn cùng pha:
k=0: cực đại trung tâm
k=1 : cực đại thứ 1
Với 2 nguồn cùng pha : số cực đại luôn lẻ
Với 2 nguồn ngược pha : số cực đại luôn chẵn
k chọn số nguyên
Với 2 nguồn cùng pha : số cực đại luôn lẻ
Với 2 nguồn ngược pha : số cực đại luôn chẵn
Với 2 nguồn cùng pha : số cực tiểu luôn chẵn
Với 2 nguồn ngược pha : số cực tiểu luôn lẻ
k chọn số nguyên
Với 2 nguồn cùng pha : số cực tiểu luôn chẵn
Với 2 nguồn ngược pha : số cực tiểu luôn lẻ
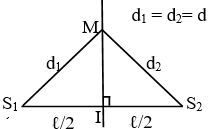
Pha tại một điểm I trên đường trung trực : (Do và )
Pha của nguồn :
Khi
Pha tại một điểm I trên đường trung trực :
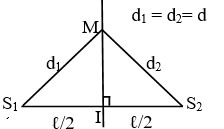
Pha tại một điểm I trên đường trung trực : (Do và )
Pha của nguồn :
Khi
Pha tại một điểm I trên đường trung trực :
Điều kiện để M là cực đại giao thoa :
Mà chạy từ M đến :
Điều kiện để M là cực tiểu giao thoa :
Mà chạy từ M đến :
Tại M có biên độ cực đại:
Vì M nằm trên đường vuông góc :
Với M có biên độ cực tiểu:
Vì M nằm trên đường vuông góc :
là đường cực tiểu hoặc cực đại nằm gần đường trung trực S1S2
Khi M nằm trên đường vuông góc với S2
Ta thay đổi và +1 thành -1
Tại M có biên độ cực đại:
Vì M nằm trên đường vuông góc :
Với M có biên độ cực tiểu:
Vì M nằm trên đường vuông góc :
là đường cực tiểu hoặc cực đại nằm gần S1
Ký hiệu là bước sóng, – là hiệu khoảng cách từ điểm M đến các nguồn sóng kết hợp và trong một môi trường đồng tính. k = 0, 1, 2,… Điểm M sẽ luôn luôn dao động với biên độ cực đại nếu:
Trong hiện tượng giao thoa sóng, hai nguồn kết hợp A và B dao động với cùng tần số và cùng pha ban đầu, số đường cực tiểu giao thoa nằm trong khoảng AB là:
Trong hiện tượng giao thoa sóng, hai nguồn kết hợp A và B dao động với cùng tần số và có độ lệch pha không đổi theo thời gian, số đường cực đại giao thoa nằm trong khoảng AB là:
Tại hai điểm A, B trên mặt nước có hai nguồn dao động cùng pha và cùng tần số . Tại điểm M cách các nguồn A, B những đoạn = , = sóng có biên độ cực đại. Giữa M và đường trung trực của AB có hai đường vân dao động với biên độ cực đại. Tốc độ truyền sóng trên mặt nước bằng:
Hai nguồn kết hợp A, B cách nhau 10cm dao động theo phương trình u = Acos100t(mm) trên mặt thoáng của thuỷ ngân, coi biên độ không đổi. Xét về một phía đường trung trực của AB ta thấy vân bậc k đi qua điểm M có hiệu số MA - MB = và vân bậc (k+5) cùng tính chất dao động với vân bậc k đi qua điểm N có NA – NB = . Tốc độ truyền sóng trên mặt thuỷ ngân là:
Trong thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp A, B dao động cùng pha với tần số . Tại một điểm M cách các nguồn A, B lần lượt những khoảng = , = . Sóng có biên độ cực đại. Giữa M và đường trung trực của AB có ba dãy cực đại khác. Tốc độ truyền sóng trên mặt nước là:
Trong thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp A, B dao động cùng pha với tần số . Tại một điểm M cách các nguồn A, B lần lượt những khoảng = , = , sóng có biên độ cực đại. Giữa M và đường trung trực của AB có hai dãy cực đại khác. Tốc độ truyền sóng trên mặt nước là:
Trong thí nghiệm giao thoa trên mặt nước, hai nguồn A, B dao động cùng pha với tần số f. Tại một điểm M cách các nguồn A, B những khoảng = , = , sóng có biên độ cực đại. Giữa M và đường trung trực của AB không có dãy cực đại nào khác. Tốc độ truyền sóng trên mặt nước là . Tần số dao động của hai nguồn là:
Trong một thí nghiệm về giao thoa sóng trên mặt nước, hai nguồn kết hợp A và B dao động với cùng tần số 50Hz, cùng biên độ dao động, cùng pha ban đầu. Tại một điểm M cách hai nguồn sóng đó những khoảng lần lượt là = , = , sóng tại đó có biên độ cực đại. Biết tốc độ truyền sóng trên mặt nước là . Số đường cực đại giao thoa nằm trong khoảng giữa M và đường trung trực của hai nguồn là:
Tạo tại hai điểm A và B hai nguồn sóng kết hợp cách nhau trên mặt nước luôn dao động cùng pha nhau. Tần số dao động . Tốc độ truyền sóng trên mặt nước là . Giữa A và B có số điểm dao động với biên độ cực đại là:
Tạo tại hai điểm A và B hai nguồn sóng kết hợp cách nhau trên mặt nước dao động cùng pha nhau. Tần số dao động . Tốc độ truyền sóng trên mặt nước là . Số điểm dao động với biên độ cực tiểu trên đoạn AB là:
Hai nguồn kết hợp A và B cách nhau lần lượt dao động theo phương trình ( cm) và (cm) trên mặt thoáng của thuỷ ngân. Xét về một phía của đường trung trực của AB, người ta thấy vân bậc k đi qua điểm M có MA – MB = và vân bậc (k +3) (cùng loại với vân bậc k) đi qua điểm N có NA – NB = . Số điểm cực đại giao thoa trên đoạn AB là:
Hai nguồn sóng kết hợp A, B cách nhau có chu kì dao động là và dao động cùng pha nhau. Tốc độ truyền sóng trong môi trường là . Số điểm cực tiểu giao thoa nằm trong khoảng giữa AB là:
Hai nguồn điểm phát sóng trên mặt nước có cùng bước sóng , cùng pha, cùng biên độ, đặt cách nhau một khoảng . Số đường dao động với biên độ mạnh nhất là:
Hai nguồn điểm phát sóng trên mặt nước có cùng bước sóng , cùng pha, cùng biên độ, đặt cách nhau một khoảng . Vẽ một vòng tròn lớn trên mặt nước bao cả hai nguồn sóng vào trong. Số điểm cực tiểu trên vòng tròn ấy là:
Thực hiện giao thoa trên mặt chất lỏng có tốc độ truyền sóng là , hai nguồn kết hợp A, B cách nhau , dao động đối pha với tần số .Số đường cực đại và số đường cực tiểu trong khoảng AB là:
Thực hiện thí nghiệm giao thoa trên mặt chất lỏng. Hai nguồn kết hợp A, B dao động đồng pha cách nhau , bước sóng là . Số điểm dao động cực đại trên biên độ AB là:
Thực hiện thí nghiệm giao thoa trên mặt chất lỏng. Hai nguồn kết hợp A, B dao động đối pha cách nhau , bước sóng là . Số điểm dao động cực tiểu trên biên độ AB là:
Thực hiện thí nghiệm giao thoa trên mặt chất lỏng. Hai nguồn kết hợp A,B dao động đồng pha cách nhau , bước sóng . Các điểm dao động với biên độ cực đại trên AB lần lượt cách A là :
Trên bề mặt chất lỏng, hai nguồn kết hợp A, B dao động ngược pha cách nhau . Bước sóng dài . Trên đường thẳng đi qua B, vuông góc với AB, nằm trên mặt chất lỏng, điểm dao động với biên độ cực đại ở gần B nhất cách B một đoạn là:
Trên bề mặt một chất lỏng, hai nguồn kết hợp A, B dao động ngược pha cách nhau . Bước sóng dài . Trên đường thẳng đi qua B, vuông góc với AB, nằm trên mặt chất lỏng, điểm dao động với biên độ cực đại ở xa B nhất cách B một đoạn:
Hai nguồn kết hợp A, B cách nhau , dao động cùng pha theo phương trình u = Acos(200t)(mm) trên mặt thuỷ ngân. Tốc độ truyền sóng trên mặt thuỷ ngân là . Điểm gần nhất dao động cùng phase với nguồn trên đường trung trực của AB cách nguồn A là:
Trên mặt chất lỏng có hai nguồn sóng kết hợp A, B cách nhau , cùng dao động với tần số và pha ban đầu bằng không. Tốc độ truyền sóng trên mặt chất lỏng là . Điểm gần nhất nằm trên đường trung trực của AB dao động cùng pha với A và B cách trung điểm O của AB một đoạn là:
Trên bề mặt chất lỏng, hai nguồn kết hợp A, B cách nhau dao động với phương trình = = acos40πt(cm,s). Vận tốc truyền sóng là . Trên đường trung trực của AB, điểm gần A nhất dao động đồng pha với A cách A một đoạn là:
Hãy giúp Công Thức Vật Lý chọn lọc những nội dung tốt bạn nhé!
Với 2 nguồn cùng pha : số cực đại luôn lẻ
Với 2 nguồn ngược pha : số cực đại luôn chẵn
Với 2 nguồn cùng pha : số cực tiểu luôn chẵn
Với 2 nguồn ngược pha : số cực tiểu luôn lẻ