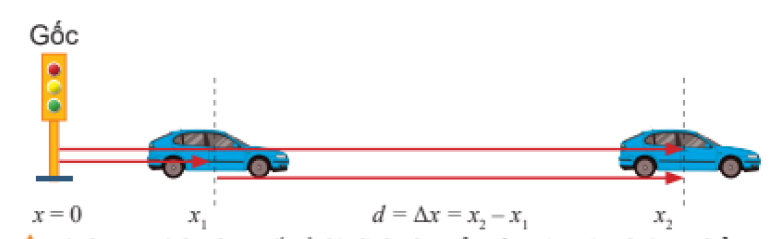Xét vật chịu tác dụng bới các lực với là góc của mặt phẳng nghiêng , là góc hợp của lực với phương chuyển động.
Theo định luật II Newton :
(công suất trung bình)
(công suất tức thời)
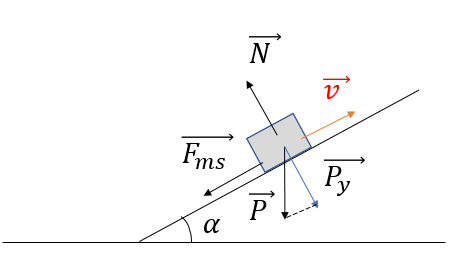
TH1 Vật đi xuống mặt nghiêng :
Chiếu lên phương chuyển động :
Chiếu lên phương Oy:
TH2 Vật đi lên mặt nghiêng :
Chiếu lên phương chuyển động:
Chiếu lên phương Oy :
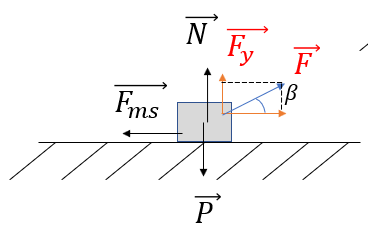
TH3 Vật đi theo phương ngang
Khi lực F hướng xuống so với phương chuyển động một góc ta thay bằng