1. Công thức tính độ biến thiên chu kì khi l, g, t thay đổi rất nhỏ - vật lý 12
Khi cả l và g đều thay đổi một lượng rất nhỏ thì:
Khi cả nhiệt độ và g thay đổi một lượng rất nhỏ thì:
2. Biên độ dài con lắc đơn sau va chạm - vật lý 12
Va chạm mềm: là sau va chạm hai vật dính chặt vào nhau
Áp dụng định luật bảo toàn động lượng:
VTCB không đổi giả sử va chạm tại li độ x:
Biên độ sau va chạm :
,V vận tốc sau va chạm
3. Công thức tính độ biến thiên chu kì của con lắc thay đổi do độ cao , độ sâu- vật lý 12
Khi đưa từ độ cao lên :
Đưa lên cao: , đưa xuống .Khi vị trí ban đầu ở mặt đất
Khi đưa từ độ sâu lên :
Đưa xuống sâu: , đưa lên .Khi vị trí ban đầu ở mặt đất
4. Công thức tính chu kì của con lắc vướng đinh - vật lý 12
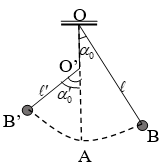
Gọi chiều dài dây treo như hình:
Dao động của con lắc gồm hai giai đoạn:
+ Nửa dao động với chu kì
+ Nửa dao động với chu kì
Chu kì dao động của con lắc
; với là chukì con lắc vướng đinh
5. Công thức tính lực căng dây của con lắc đơn - vật lý 12
Khi con lắc ở vị trí li độ góc :
Công thức
Khi góc nhỏ:
Khi vật ở biên: hay
Khi ở VTCB: hay
Chú thích :
: Lực căng dây
m: Khối lượng con lắc
g: Gia tốc trọng trường
Li độ góc
: Biên độ góc
6. Công thức tính biên độ dài và biên độ góc sau khi vướng đinh - vật lý 12
Gọi là biên độ góc cực đại ứng với chiều dài dây là ;
là biên độ góc cực đại ứng với chiều dài dây là
Gọi là biên độ dài cực đại ứng với chiều dài dây là ;
là biên độ dài cực đại ứng với chiều dài dây là
Công thức :
;
Chứng minh :
7. Công thức tính độ biến thiên chu kì con lắc đơn do nhiệt độ - vật lý 12
Khi nhiệt độ thay đổi từ đến :
Công thức
Với là hệ số nở dài
Khoảng thời gian nhanh, chậm :
8. Công thức tính độ biến thiên chu kì theo nhiệt độ và độ cao - vật lý 12
+ Khi đưa con lắc ở mặt đất (nhiệt độ ) lên độ cao (nhiệt độ ):
Với Chu kì chạy đúng
độ sai lệch
hệ số nở dài
h: độ cao
: Bán kính Trái đất
9. Công thức tính lực phục hồi của con lắc đơn - vật lý 12
Lực hồi phục của con lắc đơn là hợp lực của lực căng dây và trọng lực giúp con lắc đơn dao động điều hòa.
Công thức:
Tại biên lực phục hồi cực đại
Tại VTCB lực phục hồi bằng 0
Chú thích:
: Lực phục hồi của con lắc đơn
Li độ góc
Li độ dài
Tốc độ góc của dao động con lắc đơn
10. Lực căng dây cực tiểu của con lắc đơn - vật lý 12
hay
Khi vật ở Biên: hay
Chú thích :
: Lực căng dây
m: Khối lượng con lắc
g: Gia tốc trọng trường
Li độ góc
: Biên độ góc
11. Lực căng dây cực đại của con lắc đơn - vật lý 12
hay
Khi ở VTCB: hay
Chú thích :
: Lực căng dây
m: Khối lượng con lắc
g: Gia tốc trọng trường
Li độ góc
: Biên độ góc
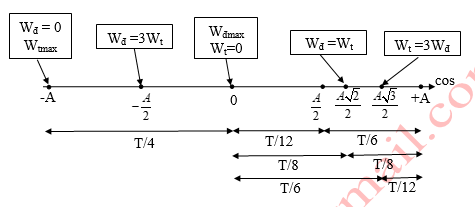
12. Tỉ số động năng và thế năng con lắc đơn - vật lý 12
Công thức :
13. Động năng của con lắc đơn - vật lý 12
Định nghĩa : năng lượng mà con lắc có được dưới dạng chuyển động.Động năng biến thiên điều hòa theo t với chu kì
Công thức :
Chú ý : Động năng cực đại ở VTCB, cực tiểu ở biên.
Chú thích:
Động năng của con lắc đơn .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dài của dao động con lắc
Độ cứng của lò xo .
Li độ dài của dao động con lắc
Pha ban đầu
14. Thế năng của con lắc đơn - vật lý 12.
Định nghĩa : năng lượng mà con lắc có được do được đặt trong trọng trường.Thế năng biến thiên điều hòa theo t với chu kì
Công thức :
Chú ý : Thế năng cực đại ở biên, cực tiểu ở VTCB.
Chú thích:
Thế năng của con lắc đơn .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dài của dao động con lắc
Độ cứng của lò xo .
Li độ dài của dao động con lắc
Pha ban đầu
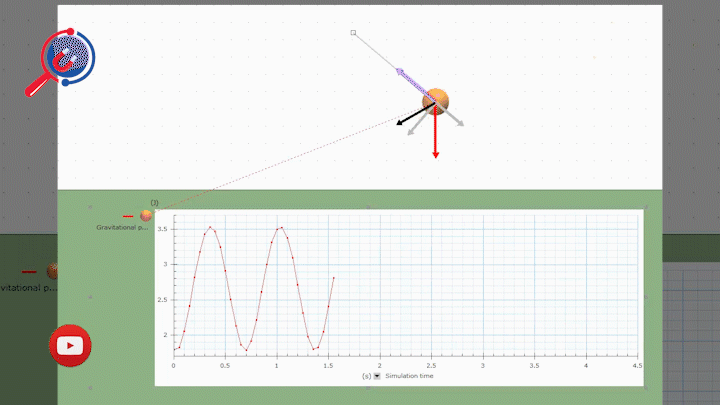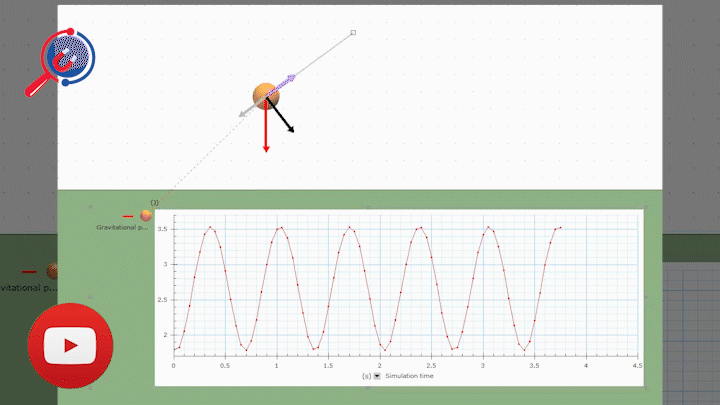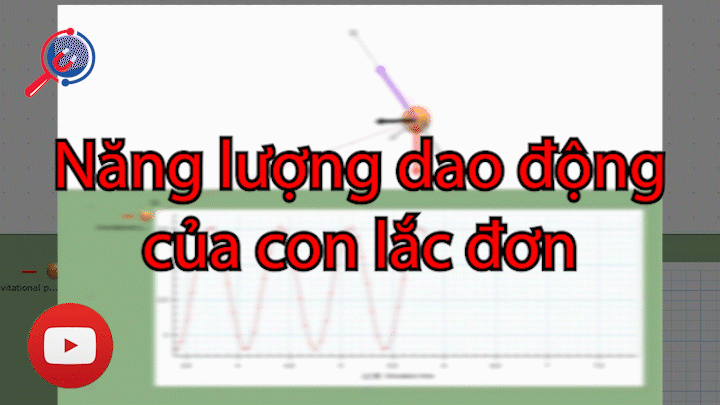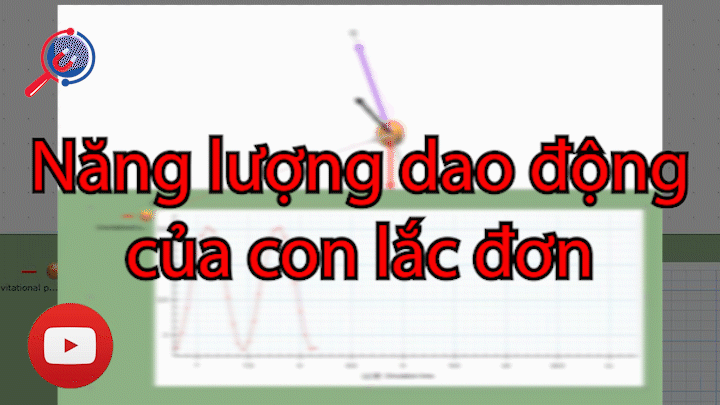
15. Cơ năng của con lắc đơn - vật lý 12
Định nghĩa : Tổng các dạng năng lượng mà con lắc có được .Cơ năng có giá trị xác định (không biến thiên theo t) và bảo toàn khi bỏ qua ma sát.
Công thức :
Chú ý : Động năng cực đại ở VTCB, cực tiểu ở biên.
Chú thích:
Cơ năng của con lắc đơn
Động năng của con lắc đơn .
Thế năng của con lắc đơn .
Khối lượng của vật .
Vận tốc của vật .
Biên độ dài của dao động con lắc
Tốc độ góc của con lắc .
Biên độ dài của dao động con lắc
Chiều dài dây treo
g: gia tốc trọng trường
16. Phương trình li độ dài , li độ góc của con lắc đơn - vật lý 12
Phương trình li độ dài , li độ góc của con lắc đơn
Với Li độ dài
Biên độ dài
Li độ góc
Biên độ góc
Tần số góc con lắc đơn
Chú ý :
+ Li độ dài , li độ góc cùng pha cực đại tại biên và bằng 0 tại VTCB.
+ Với góc nhỏ ta có hệ thức :
17. Điều kiện của đõng hồ chạy đúng do nhiệt độ và độ cao - vật lý 12
Điều kiện để đồng hồ chạy đúng:
18. Thời gian ngắn nhất để vật thỏa yêu cầu bài toán - vật lý 12
Thời gian ngắn nhất để vật thỏa yêu cầu bài toán
Bước 1 : Xác định vị trí ban đầu xét.
Bước 2 : Xác định vị trí lần đầu vật thỏa yêu cầu bài toán
Bước 3 : Tính góc quay suy ra , Với là góc quay
Hoặc dùng VTLG:
19. Công thức tính vận tốc của con lắc đơn - vật lý 12
;
Công thức:
hay
+ tại VTCB
+ tại 2 biên
Với góc nhỏ :
Hoặc
Chú thích:
Vận tốc của con lắc .
Gia tốc trọng trường .
Chiều dài dây .
Li độ góc
Biên độ góc
20. Công thức xác định chu kì của con lắc đơn trong dao động điều hòa.
Chú thích:
: chu kì dao động
: chiều dài dây treo
gia tốc trọng trường
21. Phương trình vận tốc của con lắc đơn - vật lý 12
Phương trình vận tốc của con lắc đơn
Với Li độ dài
Biên độ dài
Li độ góc
Biên độ góc
Tần số góc con lắc đơn
Vận tốc của con lắc đơn
Chú ý :
+ Vận tốc vuông pha li độ dài và li độ góc, cực đại tại VTCB và bằng 0 tại Biên.
+ Với vận tốc cực đại :
22. Phương trình gia tốc của con lắc đơn - vật lý 12
Phương trình gia tốc của con lắc đơn
Với Biên độ dài
Li độ góc
Biên độ góc
Tần số góc con lắc đơn
Gia tốc của vật
Chú ý :
+ Gia tốc chậm pha li độ dài , li độ góc ; chậm pha với vận tốc , cực đại tại VTCB và bằng 0 tại Biên.
+ Với góc nhỏ ta có hệ thức : ,,
23. Công thức chu kì của con lắc thay đổi do lực Acimet -vật lý 12
Lực đẩy Acsimet :
là khối lượng riêng của môi trường vật dao động , V là thể tích vật chiếm chỗ .
Với
Khi :
Khi :
Chu kì mới :
24. Công thức tính chu kì của con lắc thay đổi bởi lực tác dụng , lực quán tính - vật lý 12
Lực tác dụng :
Lực quán tính:
Khi lực cùng chiều với trọng lực:
Lực tác dụng : Ví dụ vật bị tác dụng hướng xuống
Lực quán tính: Ví dụ thang máy đi xuống nhanh dần đều, đi lên chậm dần đều với gia tốc a
Khi lực ngược chiều với trọng lực:
Lực tác dụng : Ví dụ vật bị tác dụng hướng lên
Lực quán tính: Ví dụ thang máy đi lên nhanh dần đều ,đi xuống chậm dần đều với gia tốc a
Khi lực vuông với trọng lực:
Khi lên dốc là góc mặt phẳng nghiêng
Chu kì mới :
25. Chu kì của lắc đơn bị thay đổi do điện trường theo phương xiên - vật lý 12
Lực điện :
Với : Cường độ điện trường
Hiệu điện thế
Khoảng cách
Khi :
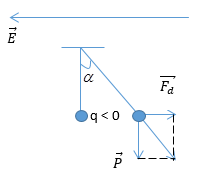
; , là góc lệch theo phương đứng
Khi
Chu kì mới :
26. Chu kì của lắc đơn bị thay đổi do điện trường thẳng đứng - vật lý 12
Lực điện :
Với : Cường độ điện trường
Hiệu điện thế
Khoảng cách
Khi : cùng phương , cùng chiều
Áp dụng khi :;
Khi : cùng phương , ngược chiều
Áp dụng khi
Chu kì mới :
27. Công thức tính thời gian nhanh chậm trong thời gian t - vật lý 12
Khi :đồng hồ chạy chậm lại.
Khi : đồng hồ chạy nhanh lên
Thời gian chạy nhanh hay chậm trong t:
Với : Thời gian đồng hồ chạy nhanh hay chậm trong t
Thời gian
Độ biến thiên chu kì
Chu kì con lắc chạy đúng
28. Công thức độ biến thiên chu kì do gia tốc hấp dẫn- vật lý 12
Với Chu kì con lắc trên thiên thể
Chu kì con lắc trên trái đất
Bán kính thiên thể
: bán kính trái đất
Khối lượng thiên thể
:Khối lượng trái đất
29. Công thức liên hệ giữa li độ dài và li độ góc - vật lý 12
Công thức:
Chú thích :
Li độ dài của con lắc đơn
Chiều dài dây treo
Li độ góc của con lắc đơn
30. Công thức tính gia tốc của con lắc đơn - vật lý 12
Gia tốc tiếp tuyến : gia tốc tiếp tuyến có phương tiếp tuyến với quỹ đạo dao động con lắc đơn
+ Công thức :
cực đại tại VTCB , cực tiểu tại biên
Gia tốc pháp tuyến :gia tốc tiếp tuyến có phương vuông tiếp tuyến với quỹ đạo dao động con lắc đơn
+ Công thức :
Gia tốc toàn phần : Tổng hợp vecto gia tốc tiếp tuyến và gia tốc pháp tuyến.
31. Công thức tính chu kì con lắc đơn theo hai chiều dài - vật lý 12
- Chu kì dao động của con lắc đơn có chiều dài và lần lượt là và thì:
Chu kì con lắc có chiều dài là
Chu kì con lắc cò chiều dài , là
Chu kì con lắc cò chiều dài , là
32. Hệ thức vuông pha cho con lắc đơn- vật lý 12
Công thức độc lập với thời gian